Eksperimentell påvisning av relativistiske effekter blir tatt som bekreftelse på at teorien er riktig. De viktigste av disse er:
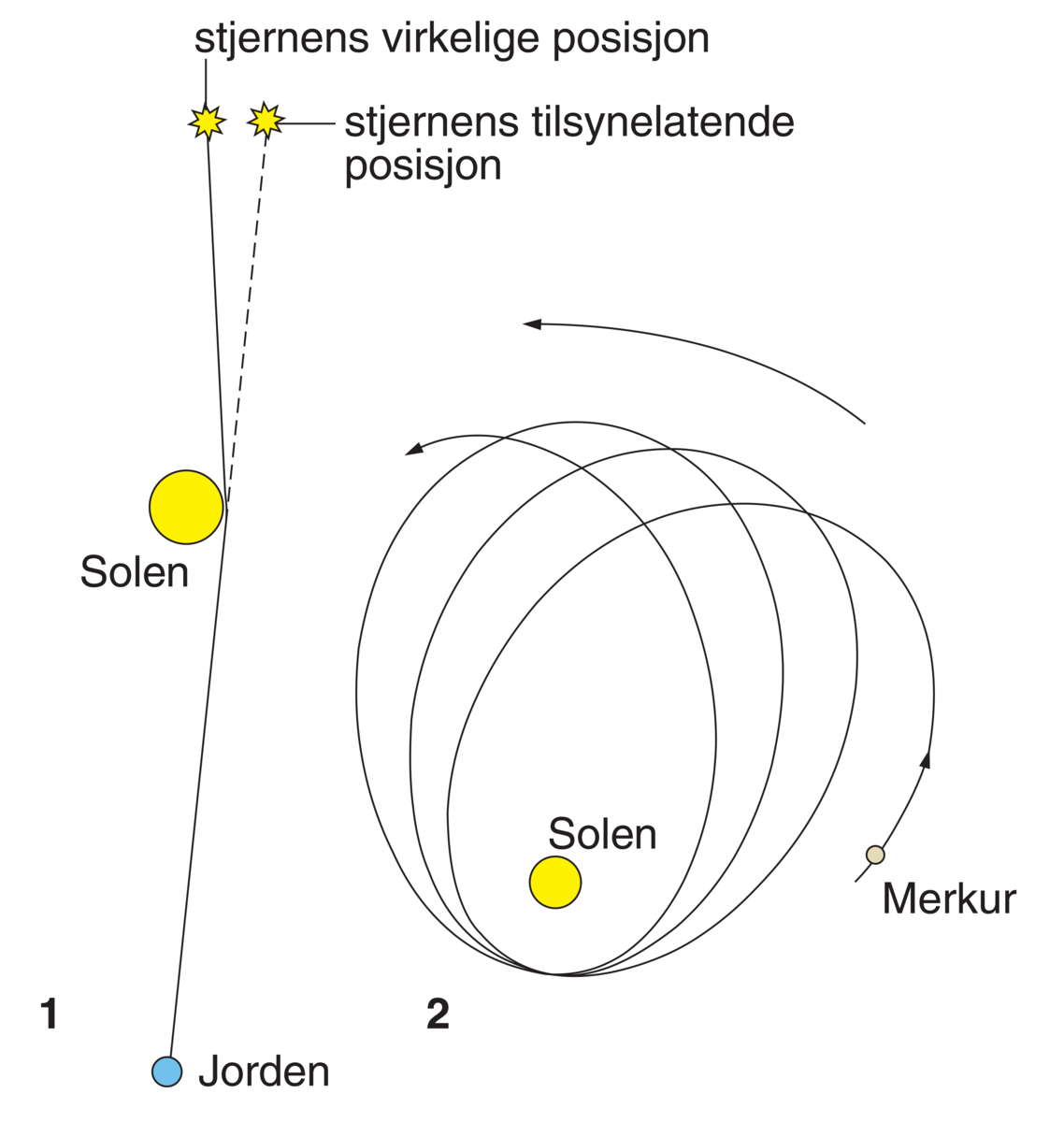
1. Merkurs perihelbevegelse. Den består i at ellipsebanen som planeten beveger seg i, dreier seg meget langsomt (se figur). Dreiningen er cirka 575 buesekunder per 100 år. Ifølge Newtons teori forårsaker de andre planetene en dreining på 532 buesekunder i samme tidsrom. Differansen på 43 buesekunder kunne ikke forklares ut fra Newtons teori, men i desember 1915 viste Einstein at relativitetsteorien forutsier en ekstra perihelforskyvning av Merkur på nettopp disse 43 buesekundene. Dette forklarte den newtonske uoverensstemmelsen mellom teori og observasjoner.
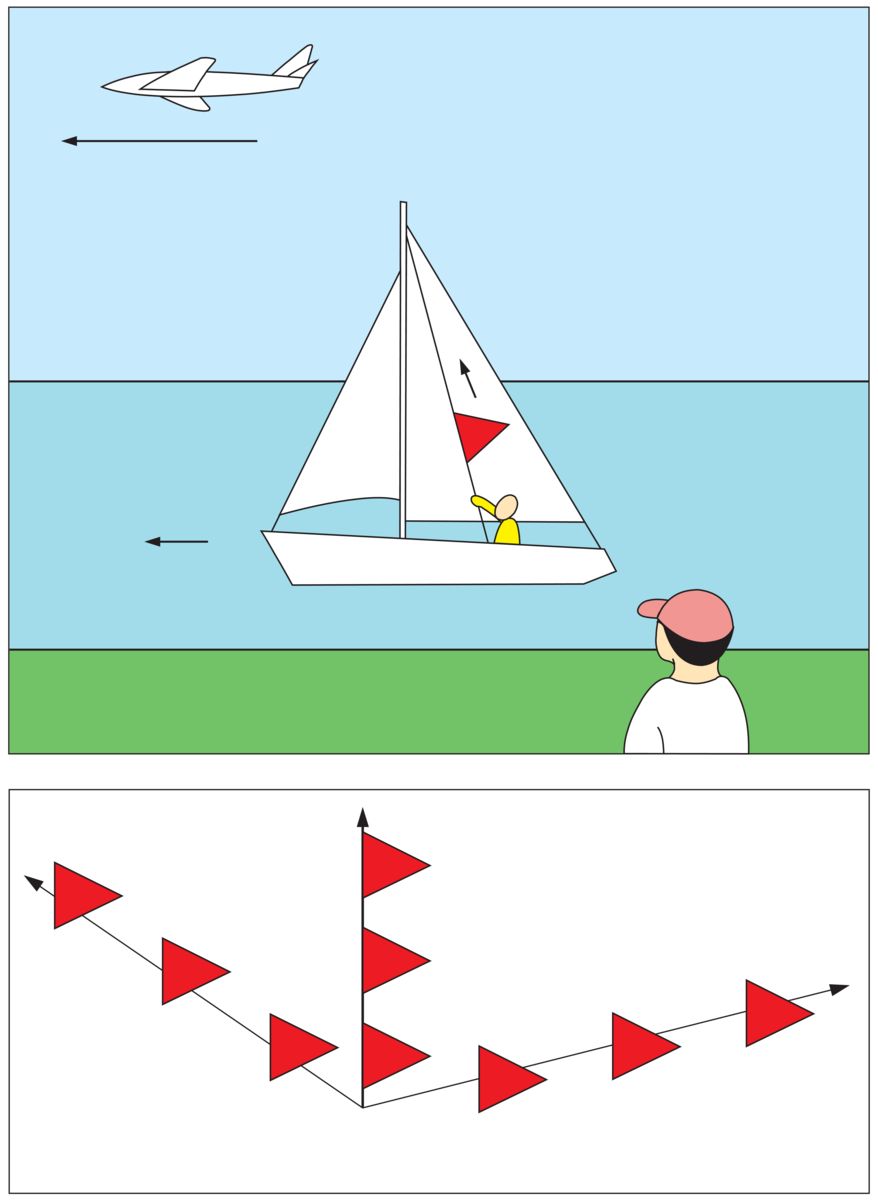
2. Lysets avbøyning i et gravitasjonsfelt kan observeres når lys fra stjerner passerer nær Solen under en solformørkelse (se figur). Avbøyningen kan være opptil 1,8 buesekunder. Den ble først påvist i 1919, siden gjentatte ganger under solformørkelser, og i senere år også ved målinger på radiobølger som passerer nær Solen. Lysavbøyningen gir også opphav til en gravitasjonell linseeffekt som opptrer når lyset fra en fjern kvasar passerer en galakse som ligger mellom kvasaren og oss. Den norske astronomen Sjur Refsdal har vist hvordan denne effekten kan brukes til å måle hvor raskt universet utvider seg.
3. Tidsforsinkelse av lyssignaler. At lys går langsommere langt nede i et gravitasjonsfelt ble for første gang målt under Shapiro-eksperimentet i 1964.
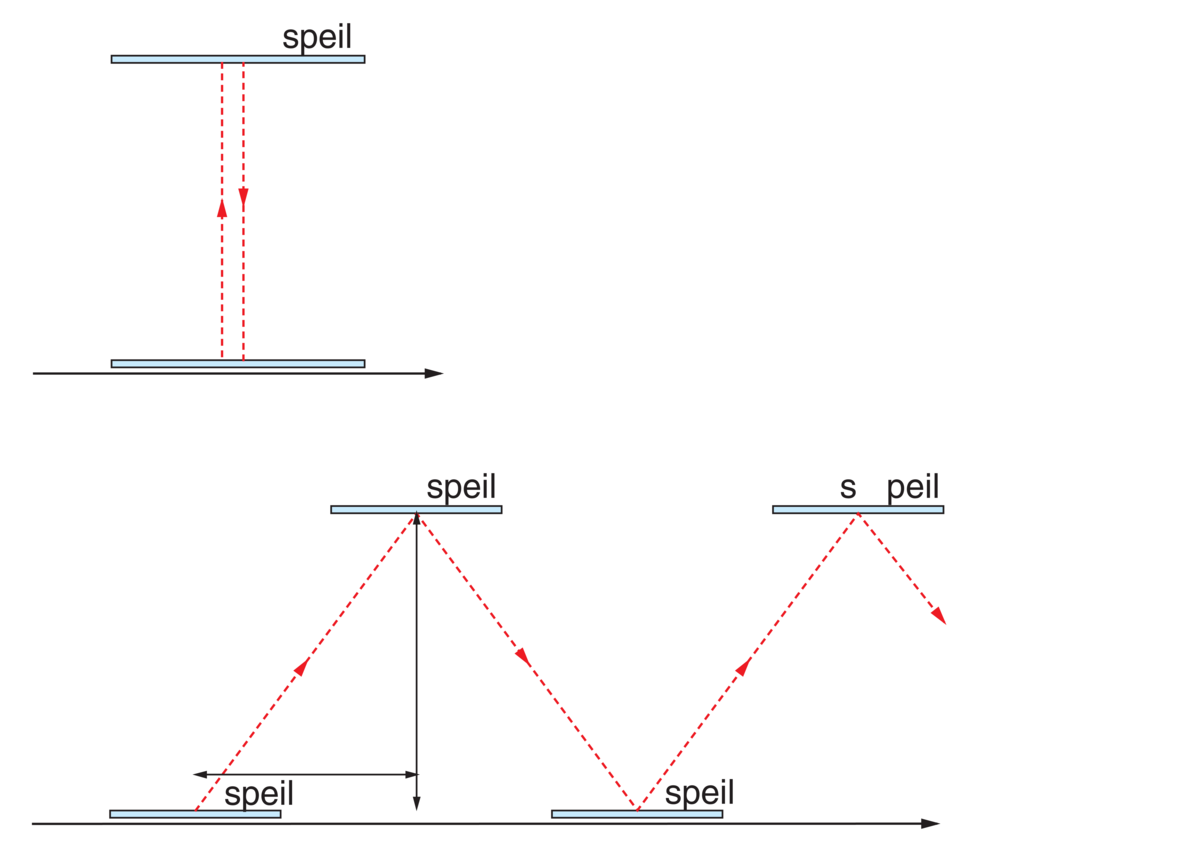
4. Gravitasjonell frekvensforskyvning av lys ble i 1960 påvist av Robert Pound og Glen Anderson Rebka ved hjelp av mössbauereffekten, hvor man sammenlignet bølgelengden til lys som ble sendt ut og absorbert med 22,5 meters høydeforskjell i Jordens tyngdefelt.
5. Gravitasjonell tidsforlengelse ble forutsagt av Einstein i 1911 og for første gang påvist eksperimentelt i Hafele-Keating-eksperimentet i 1971.
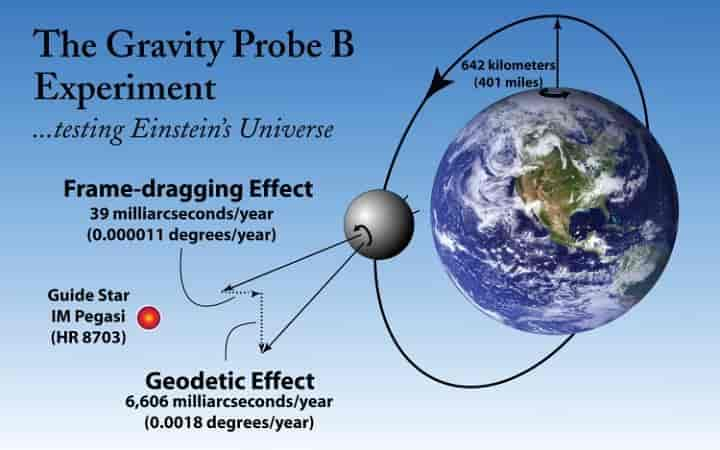
6. T reg draeffekt ble for første gang observert omkring år 2000 med LAGEOS-satellittene. Passeringspunktet over ekvator for banen til en slik satellitt som går i retning nord–sør forskyves ifølge relativitetsteorien med 13 centimeter per runde. Denne effekten ble målt, og observasjonene viste seg å stemme med teoriens forutsigelse. Effekten ble i 2008 målt i Gravity Probe B-eksperimentet (se figur). Da målte man retningsendringen av aksen til fire gyroskoper i en satellitt på grunn av den trege draeffekten. Igjen viste målingene seg å stemme med relativitetsteorien.
7. Svarte hull. I perioden 1995–2016 ble det gjort kontinuerlige målinger av bevegelsene til stjernene nær sentrum av Melkeveien. Blant annet disse observasjonene viste at det må være et såkalt supermassivt svart hull med omtrent fire millioner solmasser i Melkeveiens sentrum.
8. Frastøtende gravitasjon. I 1998 viste observasjoner av fjerne supernovaer at universets ekspansjon er akselererende. Dette er blitt forklart som en virkning av frastøtende gravitasjon forårsaket av mørk energi i universet.
9. Eksistensen av gravitasjonsbølger. Den første direkte registreringen ble gjort med den amerikanske gravitasjonsbølgedetektoren LIGO 14. september 2015, som oppfanget slike bølger fra en kollisjon mellom to svarte hull på henholdsvis 29 og 36 solmasser.





Kommentarer (1)
skrev Lars Simonsen
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.