Kinesisk matematikk er en original matematikk som fantes i Kina i 2000–3000 år (om lag år 1000 fvt.–1600 evt.) og som stort sett var isolert fra og uavhengig av samtidige babylonske, egyptiske, indiske, greske, arabiske og senere europeiske matematiske kulturer.
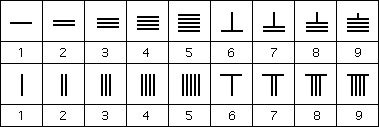
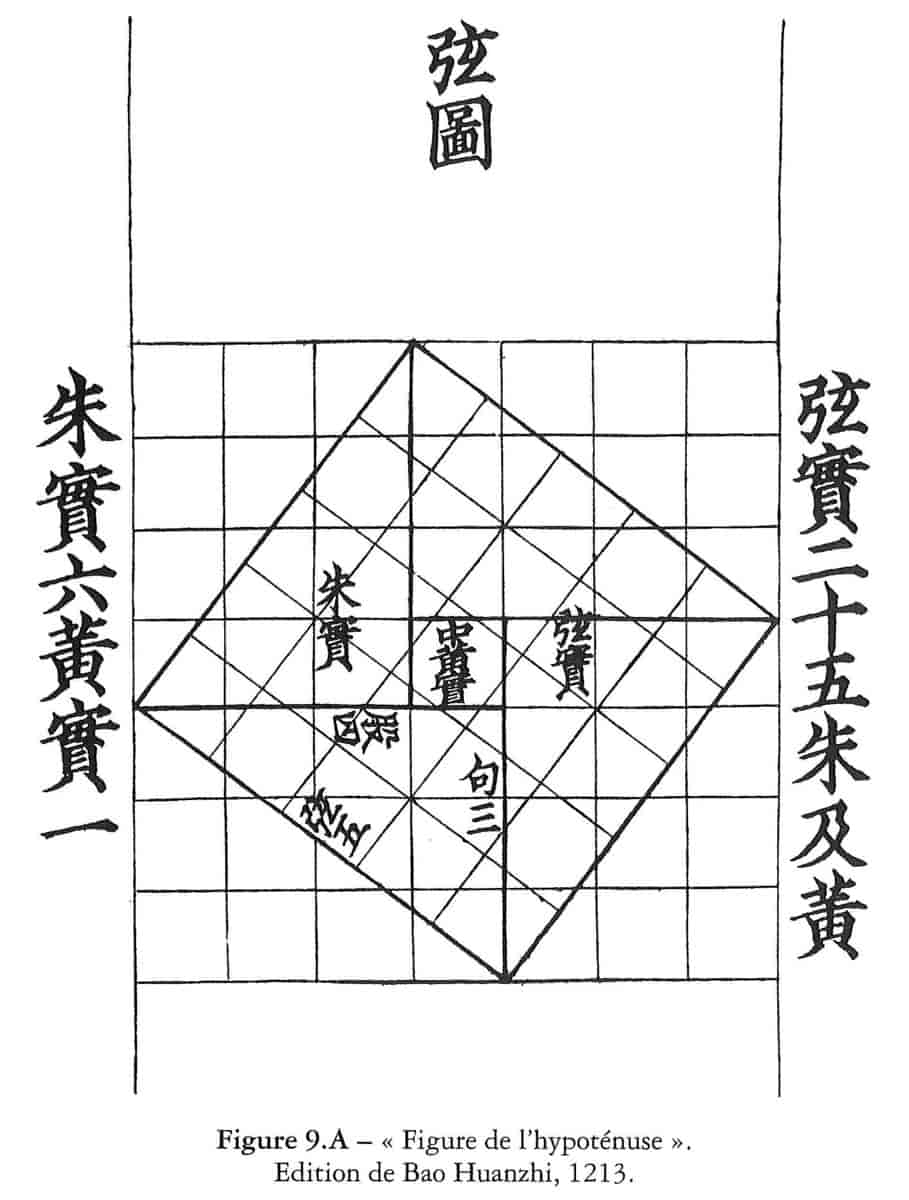
Kineserne utviklet et eget desimaltallsystem og fant mange grunnleggende numeriske algoritmer og geometriske setninger, blant dem Pytagoras’ setning. De matematiske resultatene ble alltid formulert verbalt med konkrete numeriske tall, aldri symbolsk eller abstrakt.
Den kinesiske matematikken var veldig problemorientert, mot astronomi, kalender, handel, landmåling, skatt og så videre. Kinesernes matematiske kunnskap – hvis vi betrakter matematikken som generaliserende og sammenlignende vitenskap – framgår av deres konkrete løsningsmetoder. De brukte algoritmer på en slik måte at den samme metoden (algoritmen) enten behandlet like anvendelser med forskjellige utgangstall (for eksempel beregning av trærs høyder), eller den samme metoden ble brukt i flere ulike anvendelser.
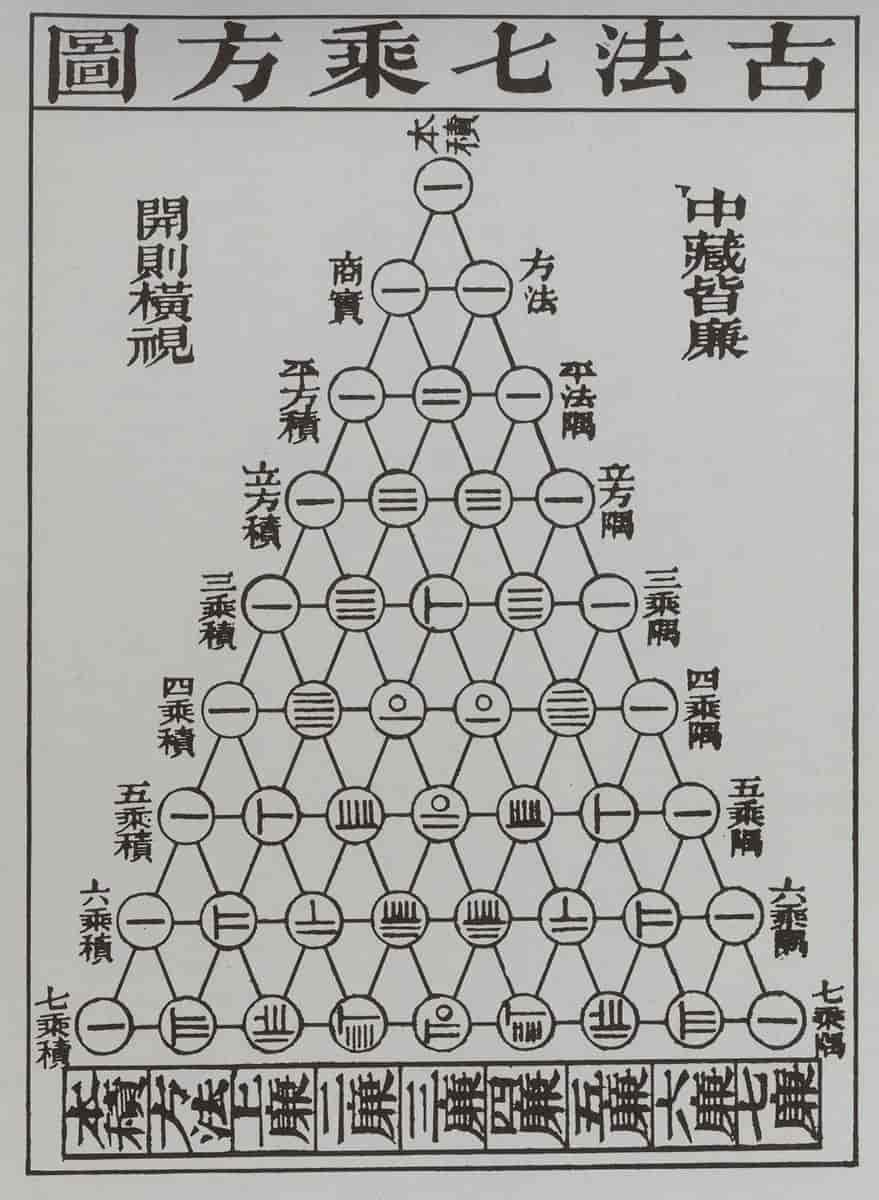
Kinesernes geometriske kunnskap framgår særlig av deres bruk av diagrammer; de sistnevnte ble oftest kun beskrevet verbalt og ikke overlevert som tegninger, før boktrykkingen startet. Det siste skjedde i Kina rundt 1000 evt., altså mye tidligere enn i Europa.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.