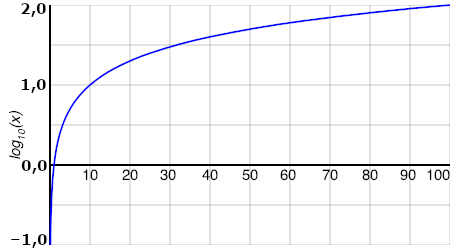
Logaritmen til et tall er det tallet et bestemt tall, grunntallet, må opphøyes i for å få det aktuelle tallet. Når g x = a, så sier man at x er logaritmen til a med g som grunntall. Dette skrives x = logg a.
For eksempel er logaritmen til 1000 lik 3 når grunntallet er 10, fordi 10 må opphøyes i 3 for å bli 1000, det vil si at 103 = 1000. Med andre ord: log101000 = 3 fordi 103 = 1000.
Det er bare positive tall man kan finne logaritmen til.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.