Akustiske målestørrelser angis som oftest i desibel, det vil si hvor mange ganger større eller mindre den aktuelle målestørrelsen er i forhold til en referanse. Når målestørrelsen er lik referanseverdien, blir dB-verdien lik 0. De ulike størrelsene har forskjellig referanse. Dersom det ikke fremgår helt klart av sammenhengen, bør derfor referansen oppgis.
-
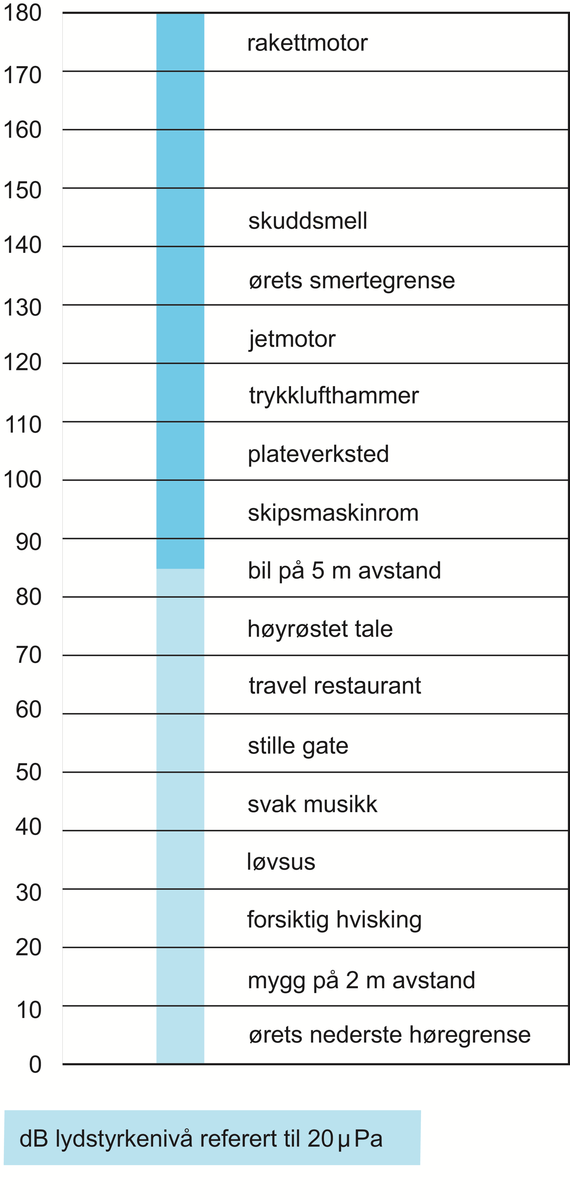
Lydtrykk måles i pascal (Pa), men oppgis gjerne i desibel i forhold til et referansetrykk på 20 µPa (20 · 10-6 Pa).
-
Lydintensitet måles i watt (W) per kvadratmeter (m2), men oppgis gjerne i forhold til en referanseintensitet på 10-12 W/m2 (1 pikowatt/m2).
- Lydeffekt måles i watt, men oppgis gjerne i desibel i forhold til en referanse på 10-12 W (1 pikowatt).
- Lydisolasjon i en vegg angis i desibel som forholdet mellom lydnivået i de to rommene på hver side av veggen.
Referansen for lydtrykk (20 µPa) tilsvarer omtrent høreterskelen. En lyd oppfattes dobbelt så sterk som en annen dersom nivåforskjellen er omtrent 10 dB.
Et lydtrykknivå på 0 dB er omtrent nedre grense for normal hørsel for en ren tone med frekvens 1000 Hz. Normal tale har et lydtrykknivå i området 30–70 dB. To lyder må ha en nivåforskjell på omkring 3 dB for at man med sikkerhet skal kunne si at de har forskjellig nivå.
Høy lyd kan være skadelig for hørselen. Smertegrensen for øret ligger omkring 130 dB, men skader kan utløses ved lavere lydnivå. Hvor mye hørselen skades vil være avhengig av en rekke faktorer, som hvor lenge en utsettes for lyd, lydens gjennomsnittlige nivå og det høyeste lydnivået.
Ørets følsomhet er frekvensavhengig. Toner i bassområdet må ha et høyere nivå enn toner i diskanten for å oppfattes som like sterke. Det benyttes derfor ulike veiekurver ved måling av lydnivå. Veiekurvene er spesifisert i standarden IEC 61672. Mest brukt er veiekurve A. Lydtrykk målt med veiekurve A angis som dBA eller dB(A). Samme notasjon benyttes for andre veiekurver. Merk at bruk av denne type suffikser ikke er godkjent i SI-systemet.
I norske retningslinjer og standarder for miljøstøy og lydforhold i bygninger benyttes hovedsakelig veiekurve A. I tilfeller der det er mye basslyd, for eksempel lyd fra tekniske installasjoner, fra diskotek og fra sprengninger og skyting med tunge våpen, benyttes også veiekurve C, som tar mer hensyn til lavfrekvente komponenter.



Kommentarer (2)
skrev Jon William Myrvoll
svarte Sverre K. Myren
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.