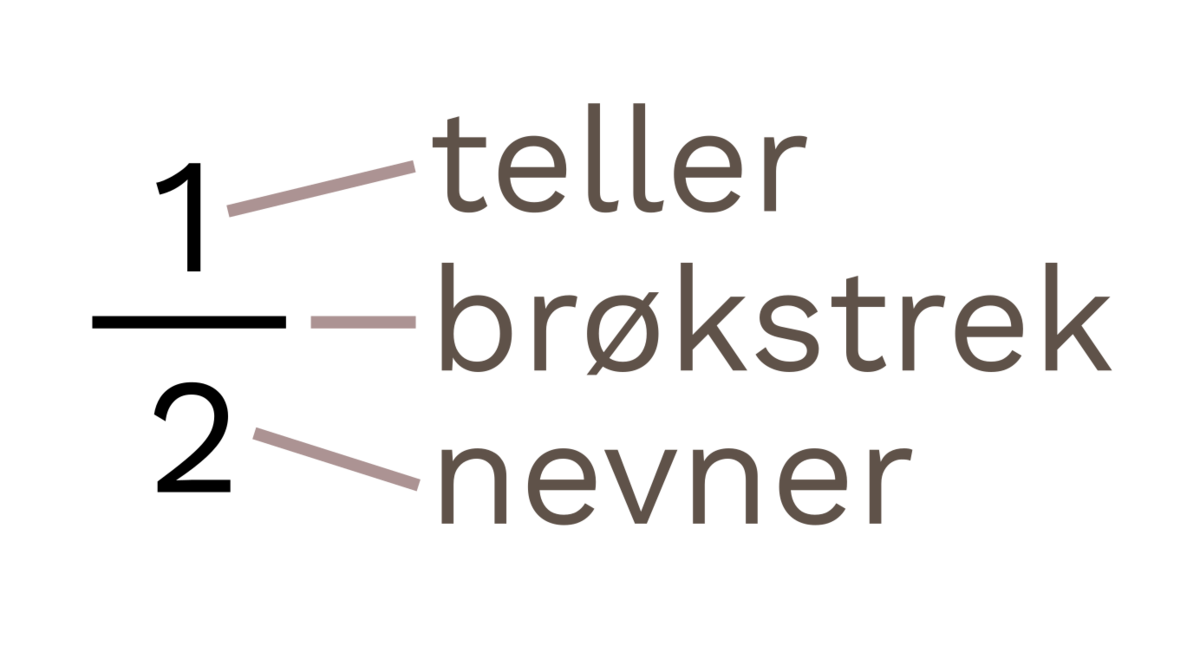
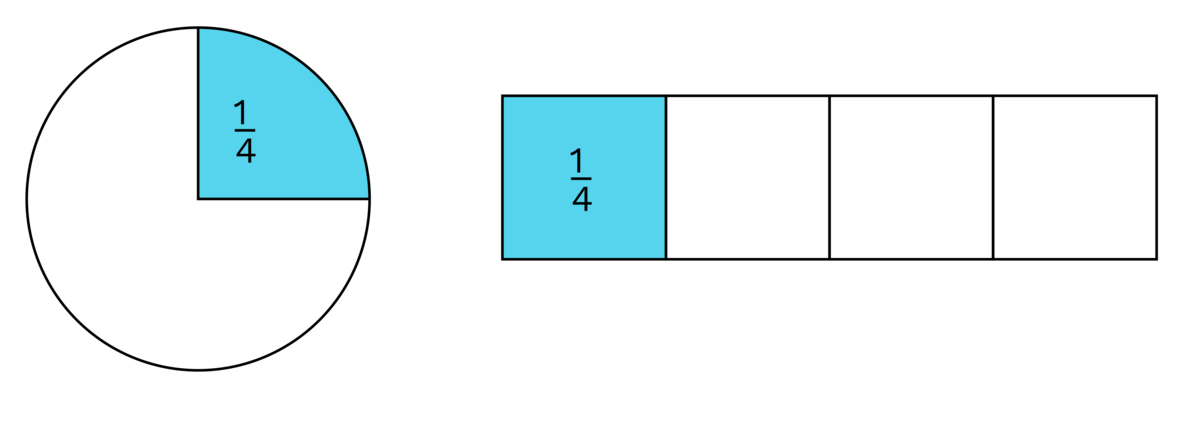
Brøk er et matematisk uttrykk for en del eller flere like store deler av en enhet. En brøk skrives vanligvis med en brøkstrek som \(\frac{a}{b}\) (eller a/b) hvor b kalles nevneren, og uttrykker hvor mange deler enheten er delt inn i (b ≠ 0), mens telleren a angir hvor mange slike deler brøken inneholder.
For eksempel er brøken \(\frac{3}{5}\) uttrykket for tre femdeler.
I en ekte brøk er telleren mindre enn nevneren, for eksempel \(\frac{2}{7}\), mens i en uekte brøk er telleren større eller lik nevneren. En uekte brøk skrives av og til som et blandet tall, det vil si som et helt tall og en ekte brøk. Eksempel: \(\frac{18}{7}\) = \(2 \frac{4}{7}\).
Bruken av brøkstrek finnes først hos Leonardo Pisano Fibonacci (ca. 1200). Brøker og heltall utgjør til sammen de rasjonale tallene.






Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.