Tall er matematiske konstruksjoner som angir mengde og størrelse. Ordet tall brukes også om talltegnene som angir disse konstruksjonene, som tegnene 0, 1, 2, 3 og så videre.
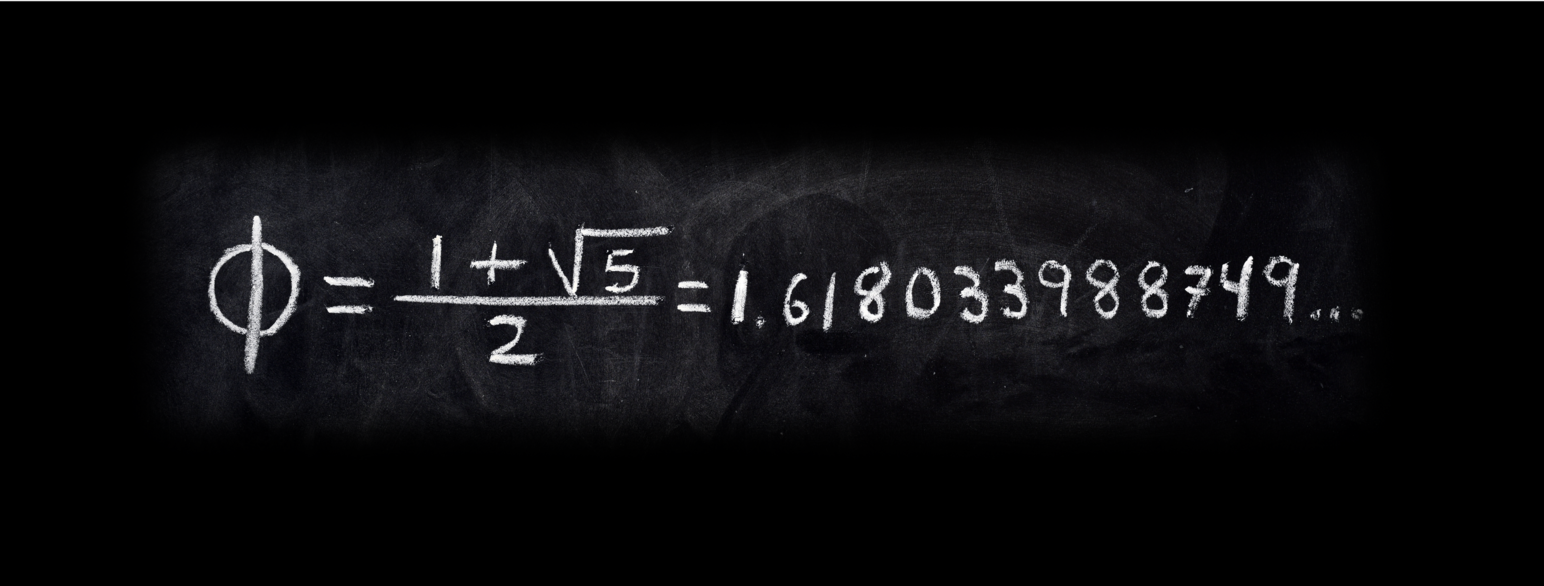
tall
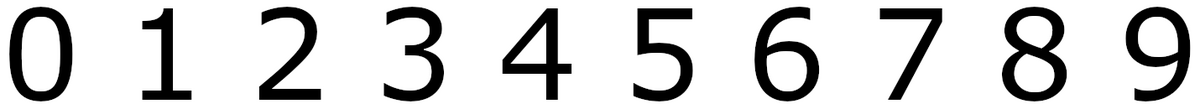
Historie
I førhistorisk tid hadde man sannsynligvis ikke noe abstrakt tallbegrep, men forholdt seg til mengder, størrelser og tidsrom ved å sammenligne med faste mengder. For eksempel kunne man vite hvor man var i en månesyklus ved å følge med på en tavle med 28 merker, og dersom man i en krukke hadde en stein for hver av sauene sine, og tok ut en stein for hver sau som kom inn, kunne man se om alle kom tilbake fra beite uten å vite hvor mange de var.
Med utviklingen av regnekunsten ble det imidlertid nødvendig med mer eller mindre symbolske måter å representere tall på (se tallsystem).
Talltegn

Vårt moderne, vestlige 10-tallsystem bruker talltegnene 0, 1, 2, 3, 4, 5, 6, 7, 8 og 9. Disse talltegnene kalles ofte arabiske, hindu-arabiske eller indisk-arabiske talltegn, da de skriver seg fra inderne og ble formidlet av araberne til Europa. Disse talltegnene fortrengte etter hvert romertallene og kom i alminnelig bruk på 1400- og 1500-tallet.
Ulike typer tall
Heltall
Den positive tallrekken 1, 2, 3, ... (de naturlige tallene) danner grunnlaget for den videre utbyggingen av tallbegrepet. Negative tall gjør det mulig å trekke fra (subtrahere) i ethvert tilfelle, og de positive og negative tallene, sammen med null (0), utgjør heltallene.
Videre innføres brøker for at divisjon (med tall forskjellig fra 0) alltid skal kunne utføres. Mengden av alle heltall og positive og negative brøker kalles de rasjonale tallene og danner en tallkropp.
Reelle og irrasjonale tall
En videre utvidelse av tallbegrepet er de reelle tallene. Ligningen \(x^2 = 2\) har ingen rasjonal løsning \(x\), og de rasjonale tallene er også mangelfulle når det dreier seg om konvergens av tallfølger. De reelle tallene består av de rasjonale tallene, og i tillegg til disse også de irrasjonale tallene, som \(i, \sqrt{2}\) og π (pi). Ved hjelp av de reelle tallene kan man representere ethvert punkt på tallinjen. Store deler av matematikken hviler på begrepet reelt tall, spesielt gjelder dette hele den matematiske analysen og mange former for geometri.
Komplekse og imaginære tall
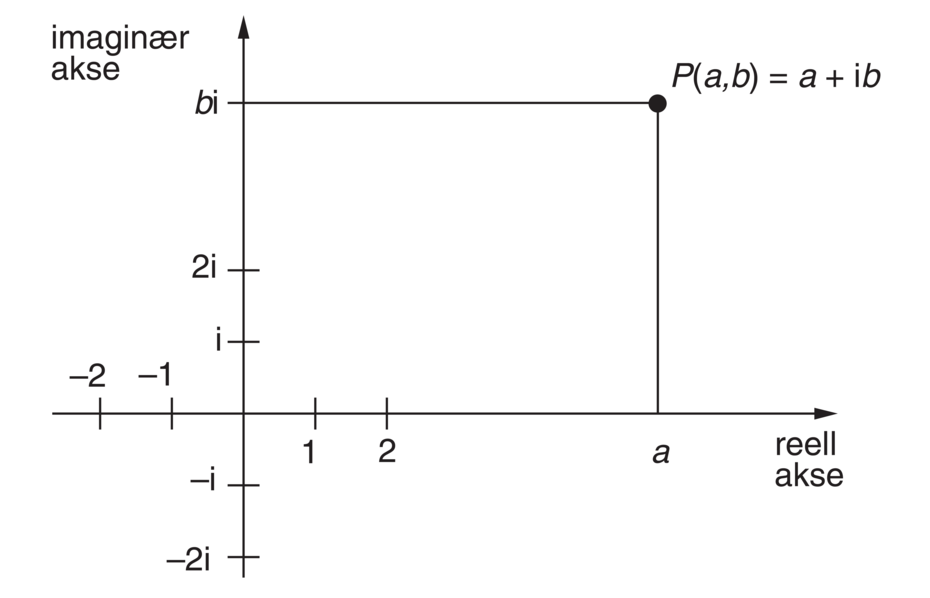
De komplekse tallene omfatter, i tillegg til de reelle tallene, de rent imaginære tallene, det vil si tall som er multipler av i, der \(i = \sqrt{–1}\). De komplekse tallene danner også en tallkropp, og har dessuten den viktige egenskapen at enhver algebraisk ligning der koeffisientene er komplekse tall, alltid har en løsning som er et komplekst tall.
Algebraiske og andre tall
En spesiell tallkropp av betydning er de algebraiske tallene, som er røttene i algebraiske ligninger med rasjonale koeffisienter. Et tall som ikke er algebraisk kalles et transcendent tall. Andre, mindre benyttede utvidelser av tallbegrepet er for eksempel hyperkomplekse tall og de p-adiske tallene (potensrekker av primtall, innført av Kurt Hensel). De såkalte transfinite tallene og kardinaltallene ble innført av Georg Cantor og spiller en stor rolle i mengdelæren.



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.