En flate i geometrien kan litt forenklet beskrives som overflaten til et legeme, eller som en oppdeling av rommet i to deler. Det er vanskelig å gi en klar matematisk definisjon som nøyaktig inkluderer de punktmengdene som naturlig regnes som flater.
flate

En flate defineres av to linjer som ikke er sammenfallende, eller minst tre punkter som ikke ligger på linje. Hvis de to linjene har ett sammenfallende punkt, vil flaten være plan. På samme måte som en linje er en uendelig rad med punkter ved siden av hverandre, kan en flate defineres som en uendelig rad med linjer. Punktene stables i én retning og linjene stables vinkelrett på den første retningen. Retningene kan også ses på som akser og dimensjoner. Fordi en flate er et punkt repetert i to retninger, har en flate to dimensjoner. Utsiden av et volum er en flate. Dette kan være en sammenhengende flate med forskjellig krumning, eller en samling av mangekanter også kalt polygoner.
Definisjon med ligninger
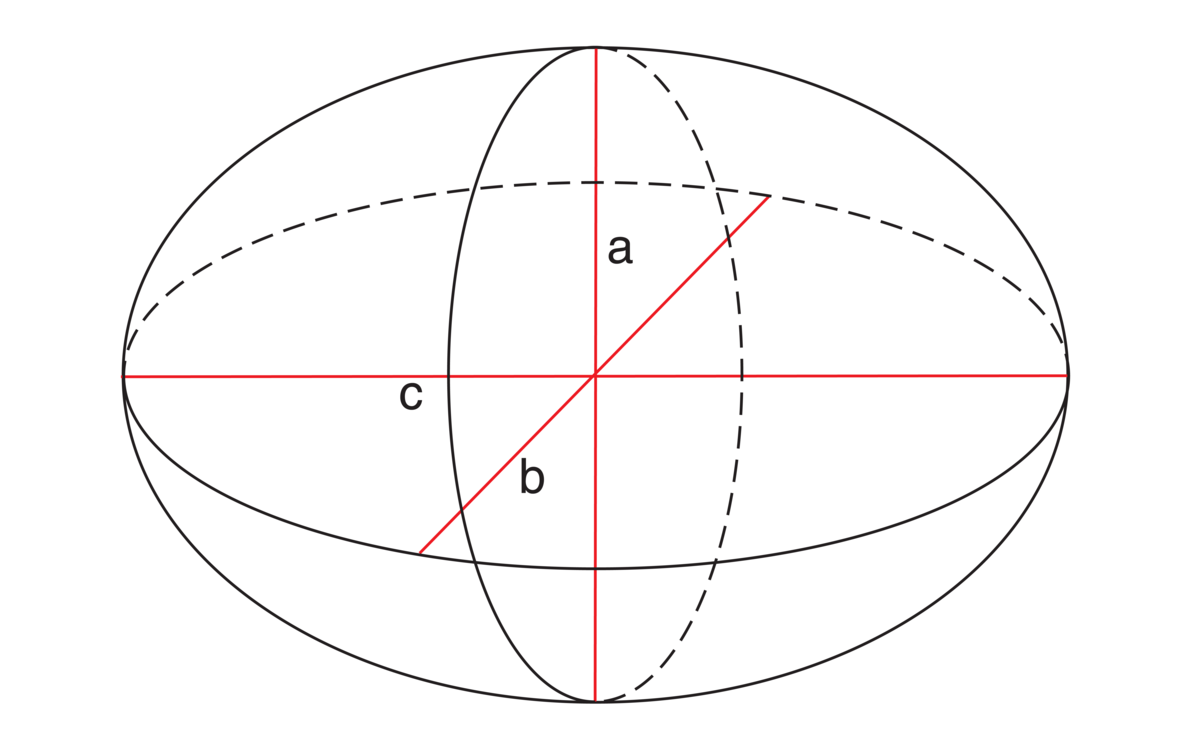
Flate. Ellipsoide med halvakser \(a, b, c\).
Flater kan defineres på forskjellig vis, ofte med noe forskjellig betydning etter de forskjellige anvendelsesområdene. I analytisk geometri og differensialgeometri defineres koordinatene til en flate ved ligninger:
\[x = f(u, v), y= g(u, v), z = h(u, v)\]
Her er \(x, y, z\) funksjoner av to parametre \(u\) og \(v\), og i alminnelighet antas de å ha (partielle) deriverte av første og annen orden. Flatens ligning kan bringes på formen \(z = f(x, y)\) eller implisitt \(F(x, y, z) = 0\).
Dersom z er en algebraisk funksjon av x og y (det vil si at F er et polynom), er flaten algebraisk; ellers er den transcendent.
Ligningen \(z = ax + by + c\) fremstiller et plan, mens \(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\) fremstiller en ellipsoide med halvaksene \(a, b, c\).
Definisjon ved en kurve
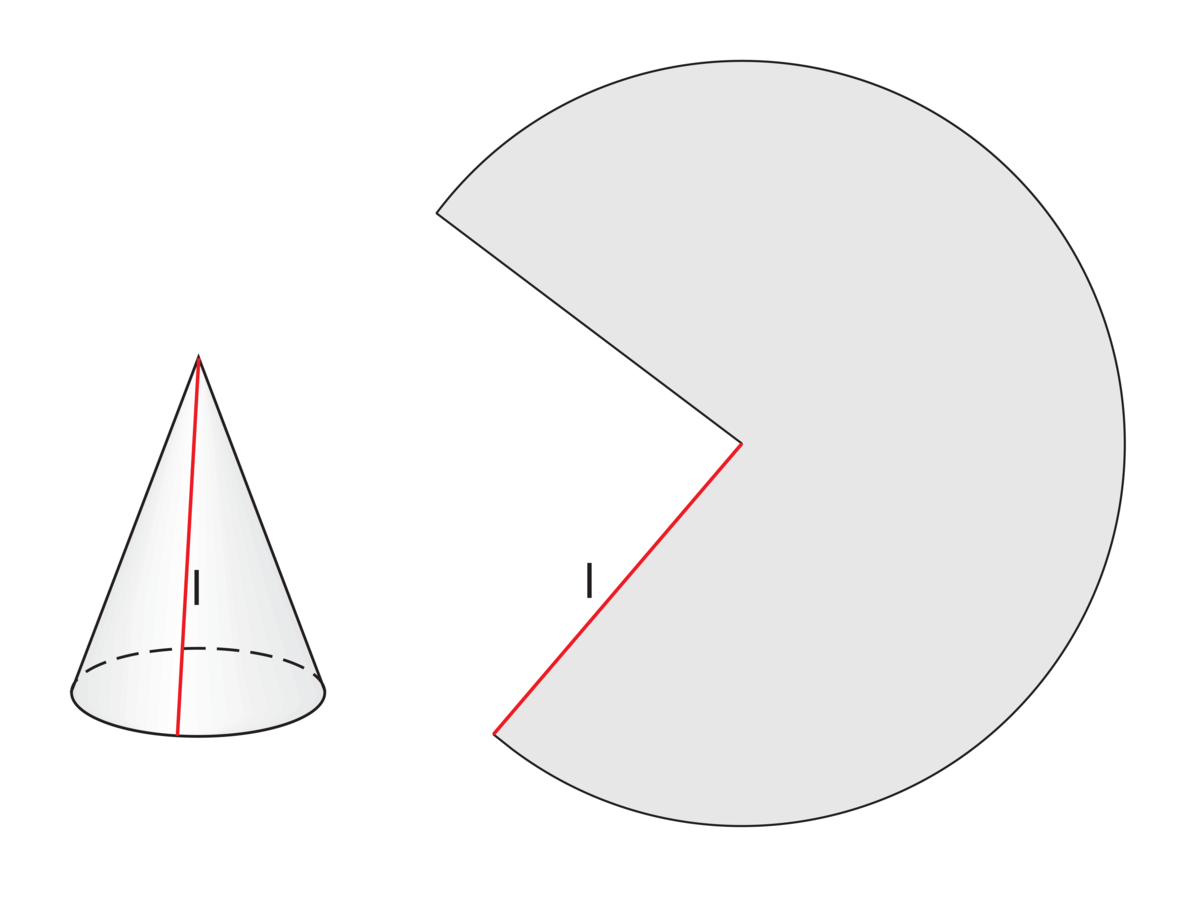
Flate. En kjegleflate kan foldes ut til et sirkelsegment.
En flate kan også defineres, eller tenkes fremkommet, ved at en kurve beveger seg i rommet. Kurven kalles da en generatrise, og hvis generatrisen er en rett linje, kalles flaten en linjeflate.
Et spesialtilfelle er utfoldelige (engelsk: developable) flater, som kan foldes ut plant uten å strekkes. Et eksempel på dette er en kjegleflate.
En omdreiningsflate oppstår når generatrisen er en plan kurve som dreies om en akse som ligger i kurvens plan.
Egenskaper ved flater
Differensialgeometrien behandler flaters tangentplan, normal, krumningsegenskaper og spesielle kurvesystemer på en flate, som geodetiske kurver.
Topologien studerer de egenskapene ved flaten som forblir uforandret ved kontinuerlige (topologiske) avbildninger. Det er for eksempel en topologisk egenskap om en flate er ensidig eller tosidig. Vanligvis forutsettes det at en flate har to sider, men möbiusbånd er et eksempel på en flate som ikke kan sies å ha mer enn én side.
Et viktig topologisk problem er å bestemme om to flater kan overføres i hverandre ved kontinuerlige en-entydige transformasjoner. Dette er for eksempel tilfellet med en kule og en ellipsoide, men ikke med en kule og en torus.



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.