Også elektrosvak teori kan beskrives av en kvantefeltteori der vekselvirkningene mellom de forskjellige fermionene, det vil si forskjellige typer leptoner og kvarker, kan beskrives som utveksling av justerbosonene (kraftformidlerne): γ (fotonet), W+, W– og Z. I motsetning til fotonet, som ikke har noen (hvile-)masse, er W± og Z svært tunge, omkring 90–100 protonmasser. Også sterk vekselvirkning mellom kvarker kan (ved energier noe større enn hvile-energien til protonet) beskrives som utveksling av ett eller flere gluoner.
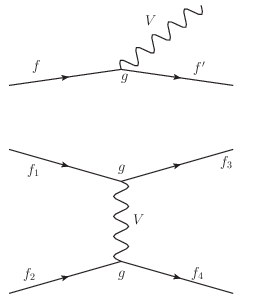
I figuren til høgre ser vi eksempel på Feynman-diagram. Øverst ser vi den fundamentale vekselvirkninga der et fermion f sender ut et vektorboson (-justerboson, kraftformidler, V) og blir til et nytt fermion f'. I QED er både f og f' et elektron, mens V er et foton \( \gamma \). Styrken i vekselvirkninga er \(g= g_\gamma =e \), der e er elementærladninga. I elektrosvak vekselvirkning kan V i tillegg til fotonet også være W± eller Z, med styrke \(e,g_W\) eller \(g_Z\), som er av samme størrelsesorden som e. Her kan f og f' være alle typer fermioner. Dersom V= W± vil forskjellen i elektrisk ladning på f og f' være \(\pm 1\). I sterk vekselvirkning (kvantekromodynamikk, QCD) er f og f' kvarker, V er et gluon og styrken er \(g_s\).
I alle disse eksempla kan ikke \( f \rightarrow V f' \) være en fysisk prosess. Men i eksemplet nederst på figuren ser vi bildet på en fysisk prosess \( f_1 + f_2 \rightarrow f_3 + f_4 \) med utveksling av vektorbosonet V , – dersom fermionene\(f_{1-4}\) er leptoner. Dersom \(f_{1-4}\) er kvarker, kan diagrammet være en subprosess der disse er inni hadroner (baryoner eller mesoner) ved kollisjoner mellom hadroner. Her kan fermionene \(f_{1-4}\) være flere typer fermioner avhengig av hva V er. Dersom V er et foton svarer dette diagrammet til et coulombpotensial \(e^2/r\) der r er avstanden mellom partiklene. Dersom V er et tungt boson som W± , svarer diagrammet til svak vekselvirkning med kort rekkevidde.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.