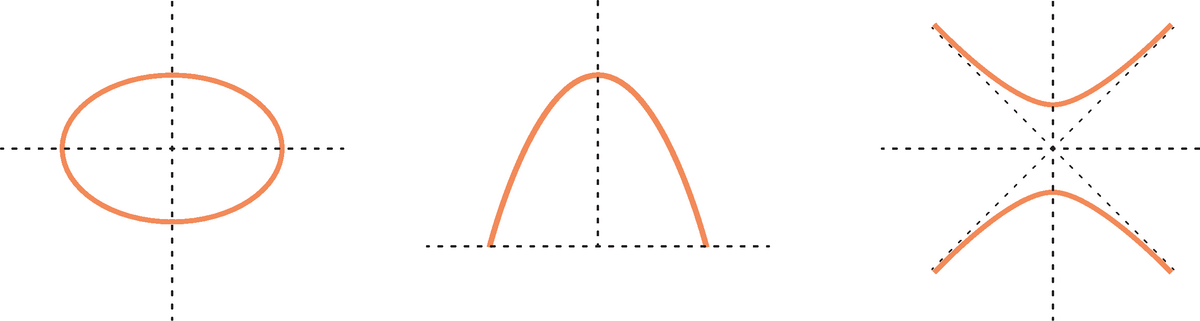
Geometrisk definisjon
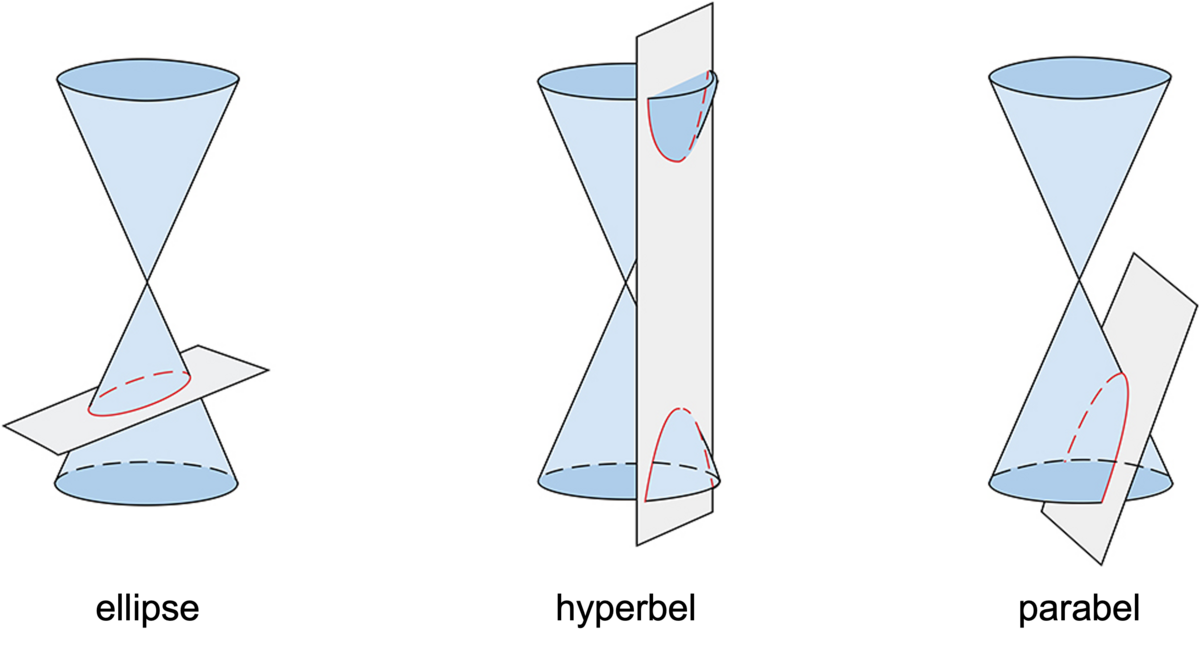
Ellipse
Når planet danner en større vinkel med aksen til kjeglen enn generatrisen gjør, vil planet skjære bare den ene halvdelen av kjegleflaten. Da er snittkurven en ellipse. Hvis planet er vinkelrett på aksen, blir kjeglesnittet en sirkel, som er et spesialtilfelle av ellipsen.
Parabel
Når planet danner samme vinkel med aksen som generatrisen gjør, skjærer planet kjegleflaten fremdeles bare i den ene delen, men snittkurven er ikke lukket. Da oppstår en parabel.
Hyperbel
Når planet danner en mindre vinkel med aksen enn generatrisen gjør, vil planet skjære begge halvdeler av kjegleflaten. Da har snittkurven to grener som til sammen danner en hyperbel.
Degenererte kjeglesnitt
Dersom snittplanet legges gjennom toppunktet til kjegleflaten, får man såkalte degenererte eller utartede kjeglesnitt. I tilfelle 1 svinner snittet inn til et punkt, en degenerert ellipse; i tilfelle 2 vil planet berøre kjegleflaten langs en rett linje, en degenerert parabel, og i tilfelle 3 er snittet to rette linjer som skjærer hverandre i kjeglens toppunkt, og de oppfattes som en degenerert hyperbel.
Analytisk definisjon
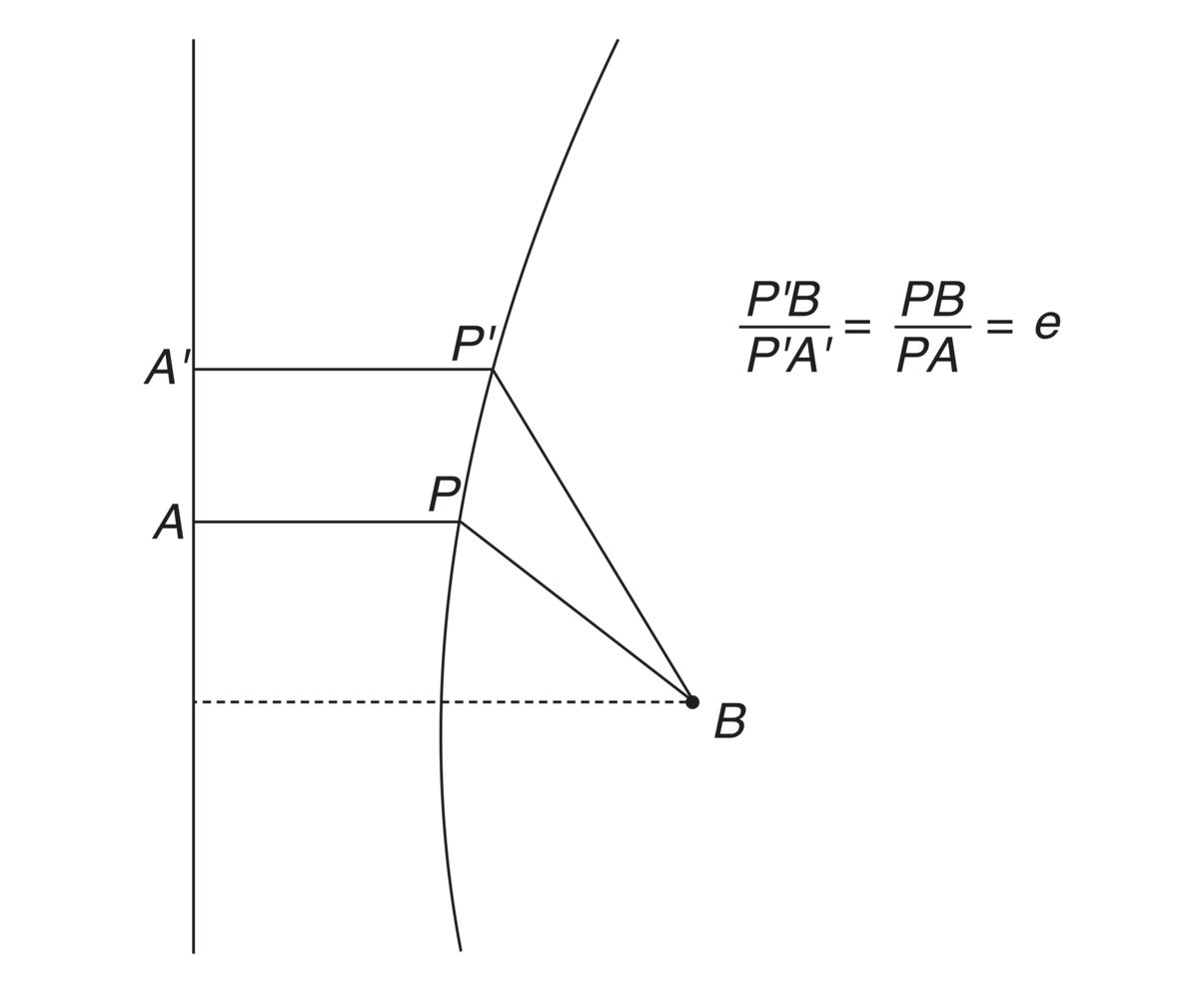
B er brennpunktet, punktene P og P' ligger på kjeglesnittkurven, og punktene A og A' ligger på styrelinjen. For alle punkter P er forholdet mellom avstanden til brennpunktet og avstanden til styrelinjen det samme tallet, e, som kalles eksentrisiteten.
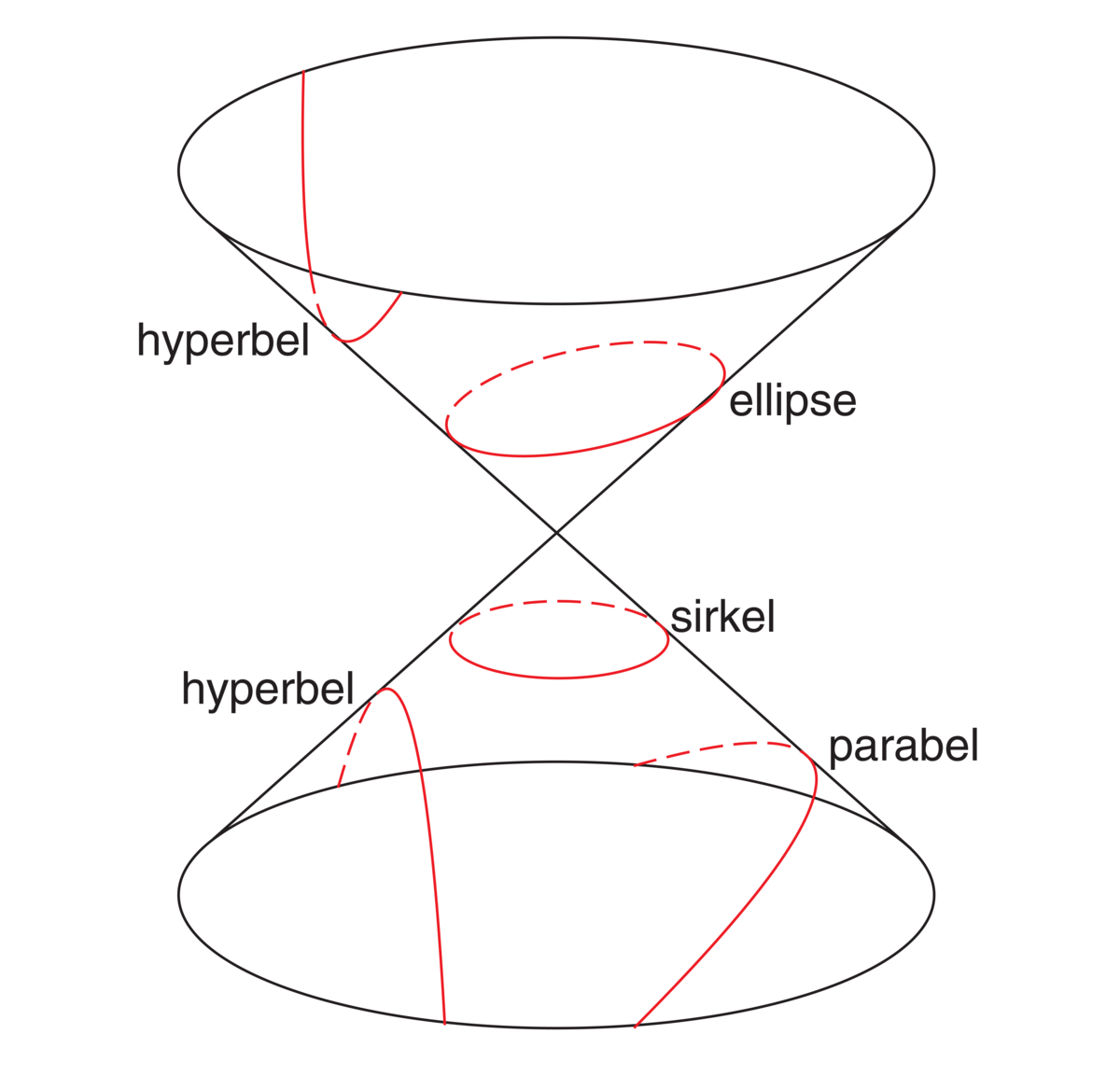
De ulike kjeglesnittene (tegnet i rødt) oppstår når et plan skjærer en kjegle i ulike vinkler.
Kjeglesnitt kan også defineres på en analytisk måte: Et kjeglesnitt er det geometriske sted for alle punkter P som ligger slik i planet at forholdet \(\frac{PB}{PL}=e\) der e er konstant. Her er PB avstanden fra P til et punkt B, brennpunktet, og PL er avstanden fra P til en rett linje L, styrelinjen (direktrisen). Forholdet e kalles kjeglesnittets eksentrisitet. Hvis e = 1 er kurven en parabel, hvis e > 1 er den en hyperbel og hvis e < 1 er kurven en ellipse. For en sirkel er e = 0.
Egenskaper
Kjeglesnittene har mange interessante egenskaper. Både ellipsen og hyperbelen har to brennpunkter og en symmetriakse som går gjennom brennpunktene, dessuten en symmetriakse som står vinkelrett på den første og går gjennom kjeglesnittets sentrum. Parabelen har bare ett brennpunkt og bare én symmetriakse. Symmetriaksen går gjennom brennpunktet.
Innenfor analytisk geometri defineres kjeglesnitt ved en ligning av andre grad \(F(x \cdot y) = 0\) mellom koordinatene \(x\) og \(y\). Kjeglesnittene er altså andregradskurver.
Hvis origo og koordinataksene velges på passende måte, kan ligningen til kjeglesnittet forenkles betydelig. For ellipsen og hyperbelen benyttes i alminnelighet sentrumsligningen:
\[\frac{x^2}{a^2}\pm\frac{y^2}{b^2}=1\]
Her faller koordinataksene sammen med kjeglesnittets akser (se ellipse og hyperbel).
En felles form for ligningen for alle kjeglesnitt er toppunktsligningen:
\[y^2 = 2px – (1 – e^2)x^2\]
Her er origo lagt i kjeglesnittets venstre toppunkt, slik at x-aksen faller sammen med kjeglesnittets akse. Her er e fortsatt eksentrisiteten, og 2p kalles kjeglesnittets parameter.
Historie
Læren om kjeglesnitt ble utviklet i oldtidens greske matematikk. Blant de første greske matematikerne som jobbet med kjeglesnitt, var Menaikhmos (rundt 350 fvt.), som benyttet kjeglesnitt i forbindelse med det deliske problem. De åtte bøkene Apollonios fra Perga skrev om kjeglesnitt er den greske matematikkens viktigste bidrag til kjeglesnittlæren. Arkimedes beskjeftiget seg særlig med arealberegninger ved kjeglesnitt.
Innføringen av analytisk geometri og infinitesimalregning brakte løsningen av alle de viktigste differensialgeometriske problemene for kjeglesnitt. En annen retning i undersøkelsene over kjeglesnitt ble skapt gjennom Jean Victor Poncelets utvikling av projektiv geometri. I denne matematiske disiplinen studerer man blant annet skjærings- og berøringsegenskaper; typiske resultater av denne sort er Pascals sats om innskrevne sekskanter i et kjeglesnitt, og Charles Julien Brianchons duale sats om omskrevne sekskanter (se dualitet).
Alle kjeglesnittene kan behandles fra et felles synspunkt innen projektiv geometri, siden man kan vise at ethvert (ikke utartet) kjeglesnitt kan transformeres projektivt til ethvert annet kjeglesnitt. Man kan også nevne definisjonen av kjeglesnitt som skjæringspunktene for tilsvarende linjer i to projektive linjebunter.




Kommentarer (3)
skrev Morten Raknes
svarte Morten Raknes
svarte Anne Eilertsen
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.