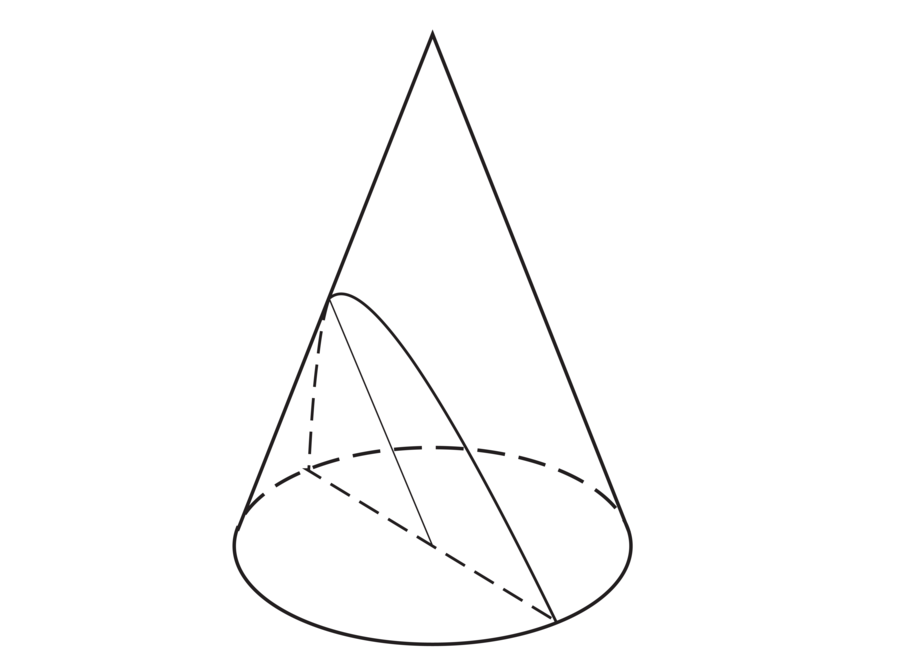
Parabel er en geometrisk kurve. Den er et kjeglesnitt som fremkommer som snittkurven mellom et plan og en kjegle hvis snittplanet er parallelt med sidelinjen (figur A).
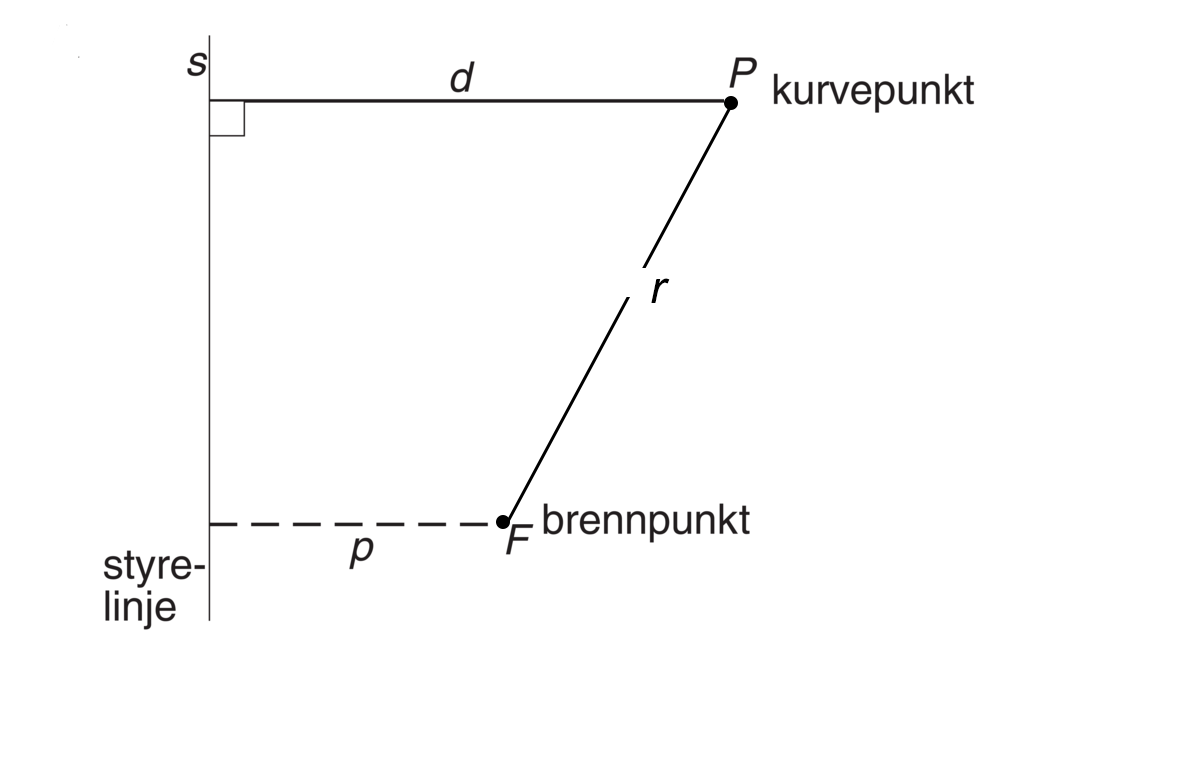
Parabelen kan defineres som en kurve der hvert punkt P på kurven har like stor avstand fra et fast punkt, brennpunktet F, som fra en fast rett linje, styrelinjen s. I figur B er altså r, brennpunktradien, like stor som avstanden d. Brennpunktets avstand fra styrelinjen kalles ofte p.
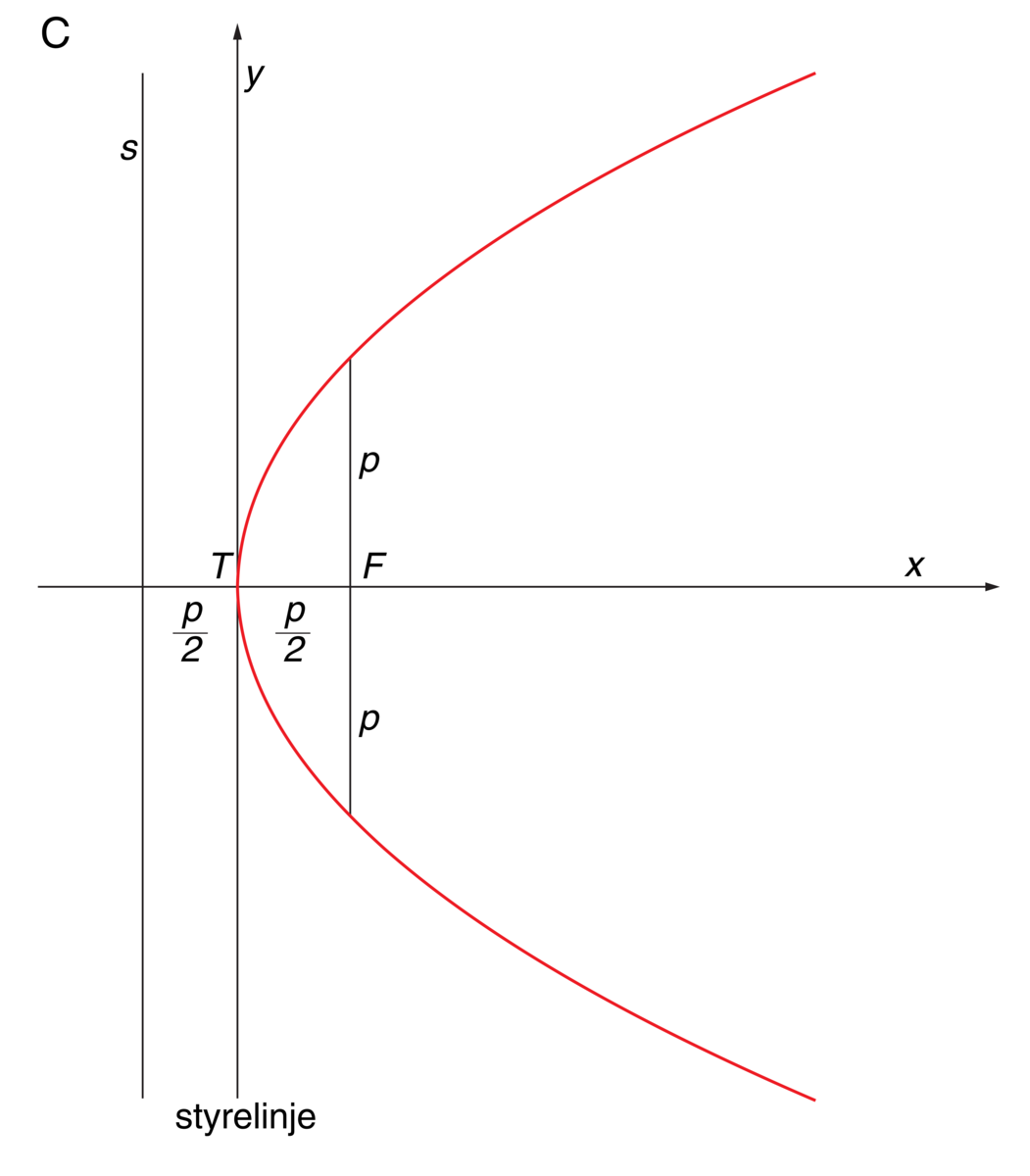
I et rettvinklet koordinatsystem hvor x-aksen går gjennom brennpunktet F vinkelrett på styrelinjen, og hvor y-aksen skjærer x-aksen midtveis mellom brennpunktet og styrelinjen, blir parabelens ligning y2 = 2px (figur C).
Av ligningen ser vi at denne parabelen er symmetrisk om x-aksen, som her også er parabelens akse, og at den er åpen i x-aksens retning. Punktet (0,0) kalles parabelens toppunkt T. Setter man inn i ligningen x = p/2, blir y = p. Størrelsen 2p i parabelens ligning er altså lengden av korden vinkelrett på x-aksen gjennom brennpunktet. Denne korden kalles parabelens parameter.
En ligning av formen y = kx2 fremstiller også en parabel med toppunkt i origo, men denne parabelens akse faller sammen med den positive delen av y-aksen når k er positiv, og langs den negative delen av y-aksen når k er negativ.
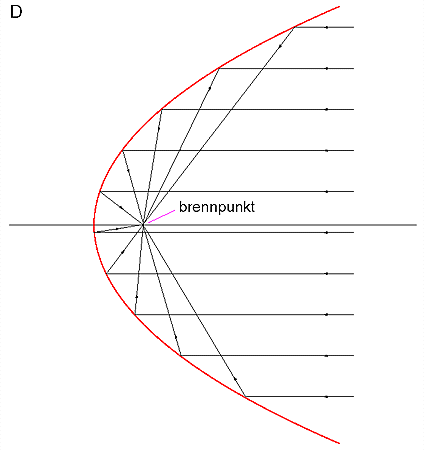
En viktig egenskap ved parabelen er at alle linjer som er parallelle med parabelens akse vil reflekteres i brennpunktet (figur D). Dette utnyttes blant annet i parabolantenner og i reflektorene i billykter.



Kommentarer (2)
skrev Magnus Skrunes
Jeg ser at i figur B er r litt større enn d. Det bør vel rettes opp.
svarte Anne Eilertsen
Takk skal du ha, vi har forsøkt å forbedre figuren.
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.