sirkel
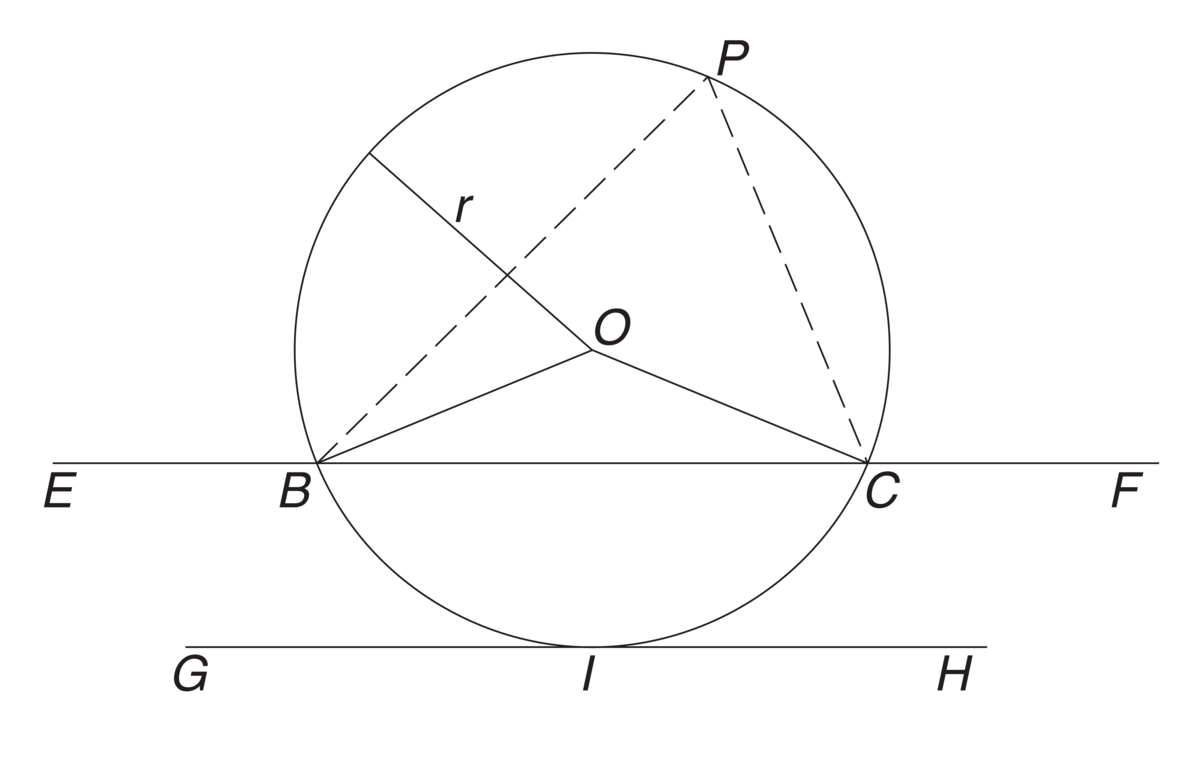
Sirkel. Sirkel med sentrum i O og radius r. Se artikkeltekst for forklaring av bokstaver og linjer.
Begreper knyttet til sirkelen
En korde er et rett linjestykke mellom to punkter på sirkelen. En sekant er en linje som skjærer sirkelen, og en tangent er en rett linje som berører sirkelen i ett punkt. I figuren vil linjestykke fra B til C være et eksempel på en korde. Den tilsvarende sekanten er hele linjen gjennom punktene, som også inkluderer punkter som E og F utenfor sirkelen. Linjen gjennom punktene G og H er en tangent med berøringspunkt I, det eneste punktet som ligger både på sirkelen og tangenten.
En del av omkretsen mellom to punkter kalles en sirkelbue, og et (sirkel-)segment er den delen av sirkelens areal som begrenses av sirkelbuen og den tilsvarende korden. En (sirkel-)sektor begrenses av to radier og sirkelbuen mellom dem. I figuren vil sirkelbuen fra B, via I, til C definere segmentet avgrenset av sirkelbuen og korden fra B til C. Sektoren bestemt av den samme sirkelbuen er avgrenset av de to radiene O til B og O til C, i tillegg til sirkelbuen selv.
En vinkel som har toppunkt i sirkelens sentrum kalles en sentralvinkel, mens en vinkel med med toppunkt på periferien kalles en periferivinkel. Periferivinkelen er halvparten så stor som den tilsvarende sentralvinkelen med samme bue. I figuren vil vinkelen i hjørnet O i trekanten OBC være en sentralvinkel, og denne vinkelen er dobbelt så stor som vinkelen i hjørnet P, en periferivinkel, i trekanten PBC.
Ligning for sirkelen

En sirkel med gitt radius \(r\) og sentrum med koordinater \((s,t)\) kan beskrives ved hjelp av Pytagoras' setning. Det gir en andregradsligning i to variabler som koordinatene \((x,y)\) til et punkt på sirkelen (altså på periferien) må tilfredsstille:
\(r^2 = (x-s)^2+(y-t)^2\)
Vi kan se at denne ligningen følger av Pytagoras' setning ved å legge inn en rettvinklet trekant i sirkelen, slik at hypotenusen er en radius, og katetene er parallelle med koordinataksene. Se figuren.
Med samme begrunnelse kan vi uttrykke sirkelen sammen med sirkelens indre ved ulikheten
\(r^2\geq (x-s)^2+(y-t)^2\).



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.