Integralregning er en viktig gren av matematisk analyse. Det å finne integralet av en funksjon kalles å integrere funksjonen, og integrasjon er den motsatte regningsarten av derivasjon. Integralregning og differensialregning kalles samlet sett for infinitesimalregning (engelsk calculus).
Faktaboks
- Uttale
- integrˈalregning
- Etymologi
- av integrere
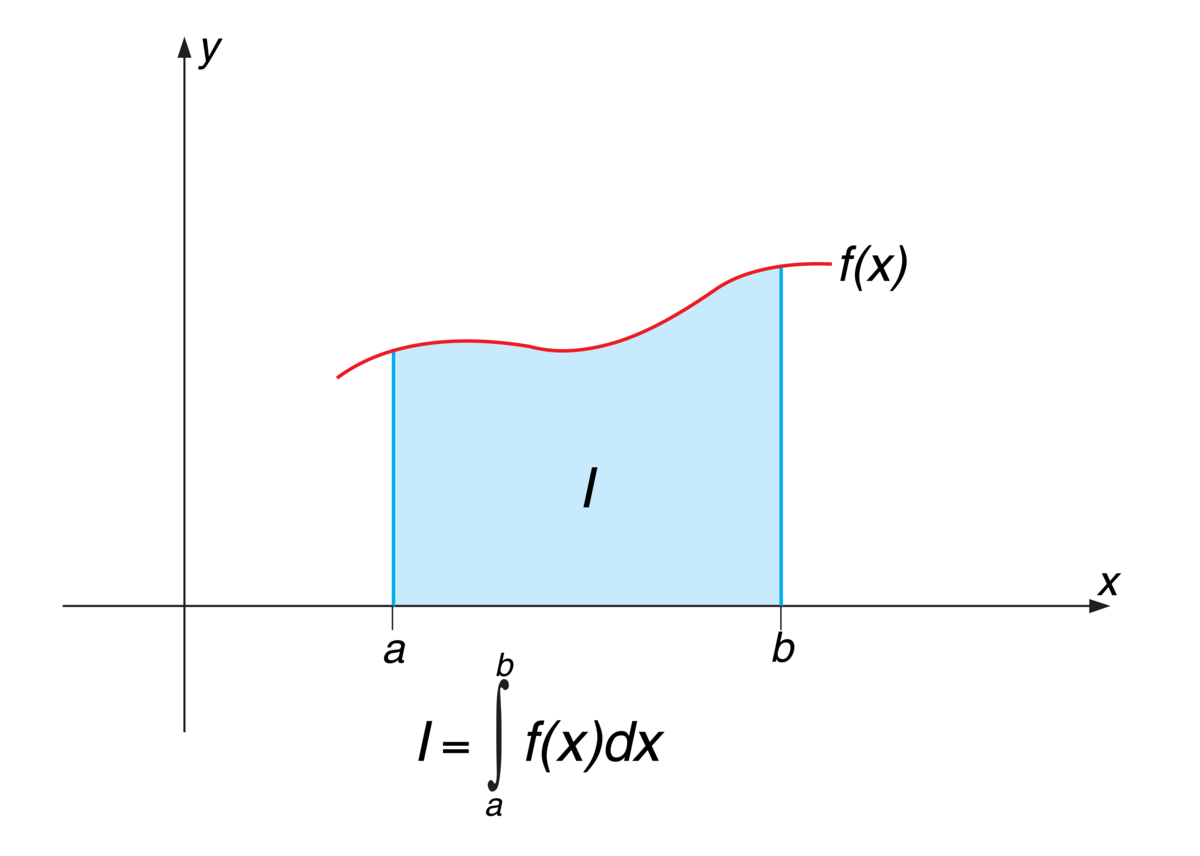
Differensialregningens utgangspunkt er å komme frem til et matematisk uttrykk for forandringer i forskjellige typer av naturprosesser, for eksempel i vekst, utvikling eller bevegelse. Integralregningens utgangspunkt er derimot å kvantifisere forskjellige typer av «totaliteter» som ikke er tilgjengelige ved vanlige elementære beregningsmåter. Dette kan gjelde arealberegninger, beregninger av volumer, masser, arbeid og så videre.
Differensialregningen og integralregningen viser altså stor ulikhet både i motivasjon og mål, men likevel er de nøye knyttet sammen ved at derivasjon og integrasjon fremtrer som motsatte regningsarter.





Kommentarer (1)
skrev Espen Løkseth
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.