For derivering har man en rekke generelle regler. Den deriverte av summen av to funksjoner \(y = f(x) + g(x)\), er \(y ʹ = f ʹ(x) + g ʹ(x)\), og den deriverte av produktet av to funksjoner \(y = f(x) \cdot g(x)\) er \(y ʹ = f(x) \cdot g ʹ(x) + g(x) \cdot f ʹ(x)\), den såkalte Leibniz' regel. Sammen med kjennskapet til den deriverte av en rekke spesielle funksjoner som for eksempel \(x^n\), \(\sin x\) og \(\cos x\), gjør disse regler at vi kan finne uttrykk for de deriverte funksjoner som opptrer i forskjellige anvendelser. Se for øvrig tabell med noen derivasjonsregler.
I stedet for \(y'\) og \(f'(x)\) bruker man også symbolet \(\frac{dy}{dx}\) hvor bokstaven \(d\) står for ordet differensial. Symbolet må imidlertid ikke oppfattes som en brøk i vanlig forstand.
Det er ofte hensiktsmessig å derivere en funksjon to eller flere ganger på rad. Den første deriverte blir da \(f'(x)\), den andre deriverte \(f''(x)\) og så videre. Om vi deriverer funksjonen \(n\) ganger, kan vi skrive det som \(y^{(n)}\) eller \(f^{(n)}(x)\).
Er en funksjon avhengig av to variabler, for eksempel \(z=f(x,y)\), kan det oppstå behov for å derivere funksjonen under den forutsetning at for eksempel \(y\) er konstant og \(x\) variabel. Da skriver man ofte resultatet slik: \(\frac{\partial f}{\partial x}\) og leser: den partiellderiverte av \(f\) med hensyn på \(x\). Om man partiellderiverer to ganger med hensyn på \(x\), skriver man dette som \(\frac{\partial^2 f}{\partial x^2}\). Dersom man istedenfor partiellderiverer én gang med hensyn på \(x\) og én gang med hensyn på \(y\), skriver man dette som \(\frac{\partial^2 f}{\partial y \partial x}\). Om funksjonen \(f\) er tilstrekkelig regulær, vil \[\frac{\partial^2 f}{\partial y \partial x}=\frac{\partial^2 f}{\partial x \partial y},\] det vil si at det ikke betyr noe i hvilken rekkefølge man foretar derivasjonene. Det er også vanlig å bruke indekser til å angi partiellderivasjon, dvs \(f_{xy}=\frac{\partial^2 f}{\partial y \partial x}\).
La oss se på eksemplet \(z=f(x,y)= x^2y^3+\sin(xy)+x+2y\). Da er \(z_x=f_x(x,y)= 2 xy^3+y\cos(xy)+1\) og \(z_y=f_y(x,y)= 3 x^2y^2+x\cos(xy)+2\). For de andrederiverte finner vi \(z_{xx}=f_{xx}(x,y)= 2 y^3-y^2\sin(xy)\), \(z_{yy}=f_{yy}(x,y)= 6 x^2 y-x^2\sin(xy)\) og \(z_{xy}=f_{xy}(x,y)= z_{yx}=f_{yx}(x,y)=6 x y^2-xy\sin(xy)\).


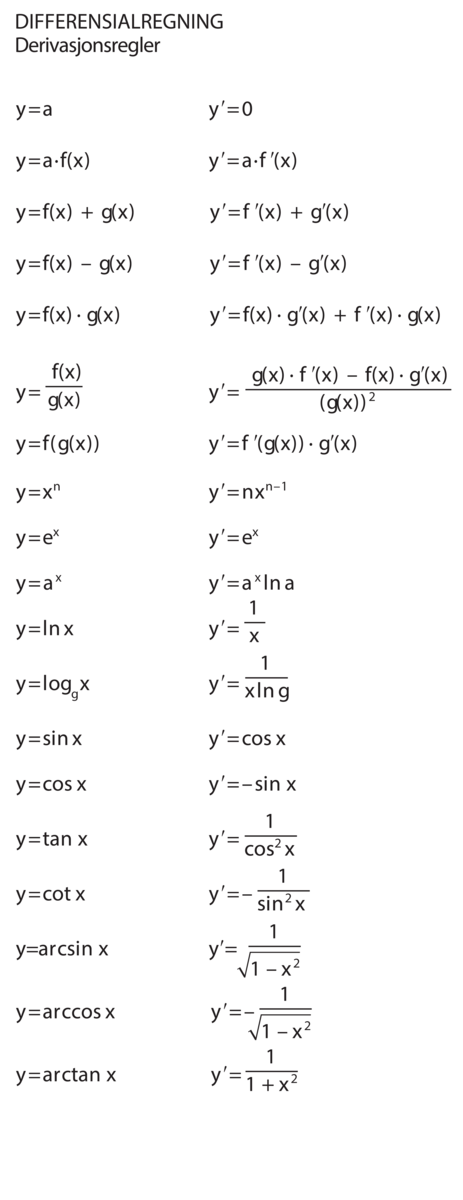


Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.