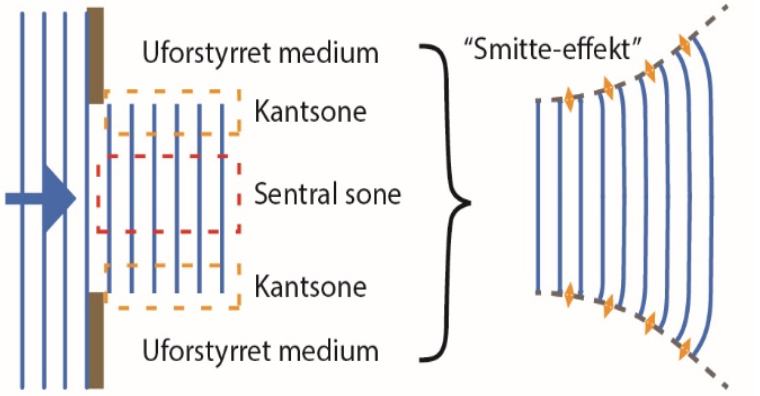
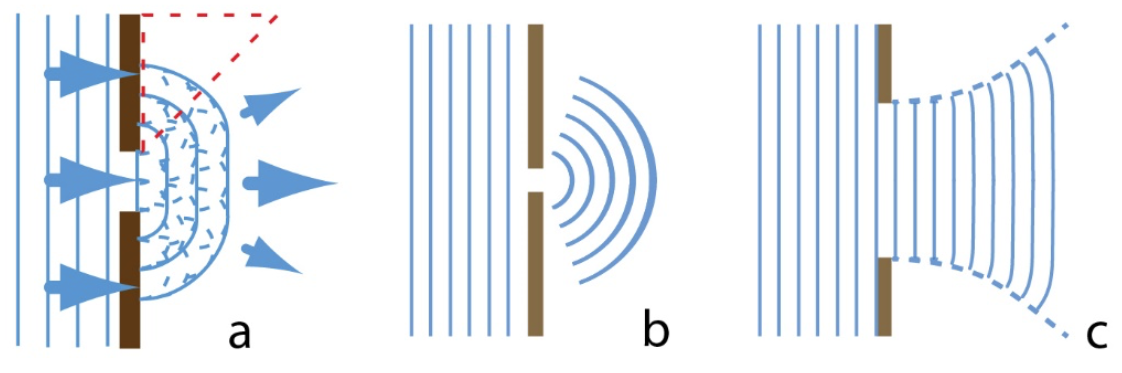
Diffraksjon er eit fenomen som skjer når bølgjer treffer ei hindring eller passerer ei opning. Det kan sjå ut som om bølgjene blir avbøygde rundt til dømes eit hjørne eller breier seg ut etter å ha passert ei spalte i ein skjerm.
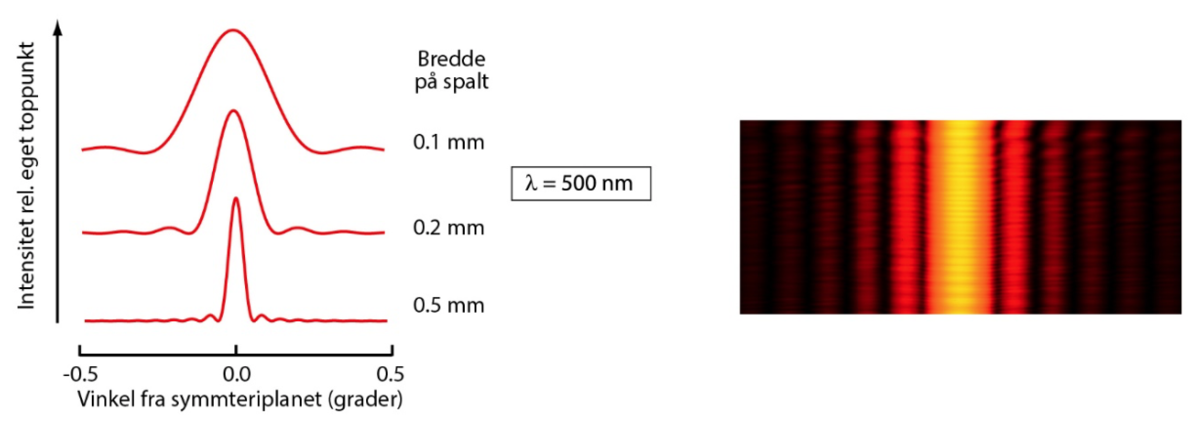
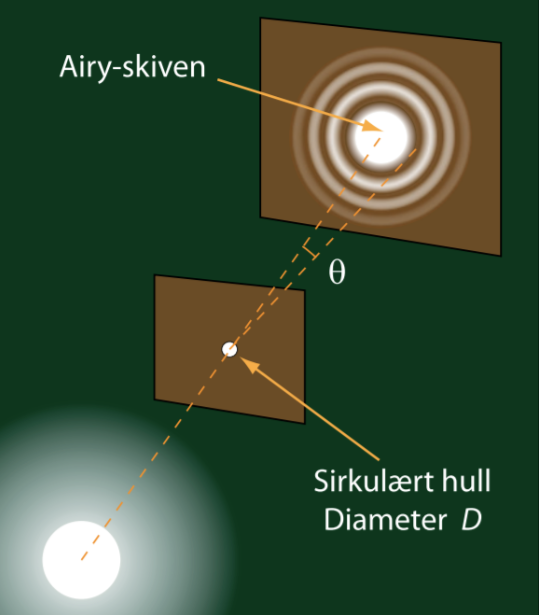
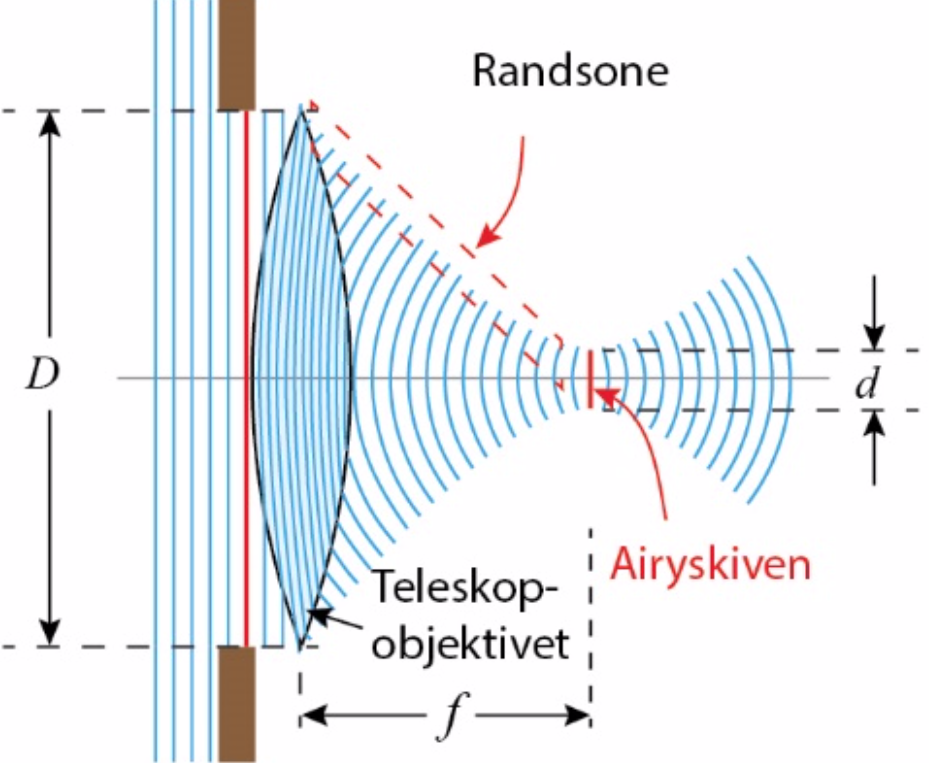
Ofte omtalar ein diffraksjon i samband med lysbølgjer, men alle typar bølgjer – til dømes lyd- og vassbølgjer eller materiebølgjene innan kvantefysikken – blir utsette for diffraksjon. Ein praktisk konsekvens av diffraksjon er at det set grenser for oppløysingsevna til optiske instrument.




Kommentarar
Kommentarar til artikkelen blir synleg for alle. Ikkje skriv inn sensitive opplysningar, for eksempel helseopplysningar. Fagansvarleg eller redaktør svarar når dei kan. Det kan ta tid før du får svar.
Du må være logga inn for å kommentere.