Schrödingerligningen er en matematisk ligning som ble utledet av Erwin Schrödinger i 1925, og som danner grunnlaget for bølgemekanikken i moderne kvantefysikk.
Faktaboks
- Uttale
- skrˈødinger–
- Også kjent som
-
Schrödingers bølgeligning
Schrödingerligningen er en matematisk ligning som ble utledet av Erwin Schrödinger i 1925, og som danner grunnlaget for bølgemekanikken i moderne kvantefysikk.
Schrödingers bølgeligning
Schrödingerligningen er en differensialligning som beskriver hvordan et kvantemekanisk system oppfører seg som funksjon av både tid og rom.
Ligningen ble publisert av den østerrikske fysikeren Erwin Schrödinger i 1926 og er av sentral betydning i kvantemekanikk.
Fysikeren Niels Bohr postulerte tidlig på 1900-tallet at elektroner i et atom bare kan bevege seg i bestemte stasjonære baner. Reglene som disse banene ble valgt ut etter, kjent som Bohrs kvantebetingelser, var formulert på rent empirisk grunnlag. Disse reglene var tilleggsbetingelser som måtte godtas i mekanikken ved siden av Isaac Newtons bevegelseslover.
I motsetning til dette kan elektronbanene utledes matematisk ved å løse schrödingerligningen. Ligningen er en såkalt egenverdiligning som bare har løsninger for bestemte verdier av parametre som inngår i beskrivelsen av bevegelsen.
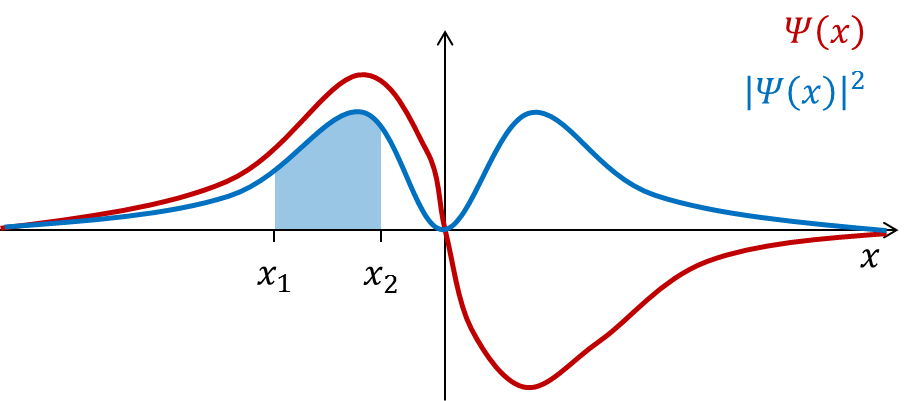
Løsninger av schrödingerligningen representerer en naturbeskrivelse som er fundamentalt forskjellig fra den som gis i klassisk (Newtonsk) mekanikk. En partikkel beskrives her ikke med bestemte koordinater i rom og tid, men med en bølgefunksjon Ψ (x, y, z, t) som representerer sannsynlighetsamplituden for partikkelen. (Ψ er den greske bokstaven psi.) Funksjonen |Ψ(x, y, z, t)|2 gir sannsynlighetsfordelingen for partikkelen i rom og tid.
Den tidsavhengige schrödingerligning for en partikkel er:
\[-\frac{\hbar^2}{2m}\nabla^2\Psi + V \cdot \Psi = i\hbar \frac{\partial \Psi}{\partial t}\]
hvor ℏ = h/2π, h er Plancks konstant, V er partikkelens potensielle energi, \(i = \sqrt{-1}\) og
\[\nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\]
er den 2. partielt deriverte med hensyn på stedskoordinatene mens
\[\frac{\partial}{\partial t}\]
er den 1. deriverte med hensyn på tiden.
Den tidsuavhengige schrödingerligningen beskriver stasjonære tilstander. I denne er både potensiell energi, V, og bølgefunksjon, Ψ, tidsuavhengige, og ligningen blir:
\[-\frac{\hbar^2}{2m}\nabla^2\Psi + V\Psi = E\Psi\]
hvor E er partikkelens totale (kinetiske og potensielle) energi.
Problemene i kvantemekanikken dreier seg ofte om å bestemme for hvilke verdier av E ligningen har løsninger, energiegenverdier, og å finne tilsvarende former for ψ, egenfunksjoner, samt å finne tilsvarende verdier av andre fysiske størrelser. Bare i spesielle tilfeller kan disse problemene løses eksakt.
Formelt kan schrödingerligningen betraktes som uttrykk for en fundamental naturlov som man kan legge til grunn for kvantefysikken. Dette ble særlig gjort i kvantefysikkens første periode. Nå betraktes den snarere som en konsekvens av kvantemekaniske prinsipper som man mener må legges til grunn for naturbeskrivelse innen atomfysikken.
I kjemi blir schrödingerligningen brukt til å beskrive fordelingen av elektroner og atomkjerner i et molekyl. Den er særlig brukt til å beregne strukturen av molekyler og hvordan molekyler reagerer med hverandre. Ligningen lar seg ikke løse eksakt for kompliserte molekyler, men den kan løses tilstrekkelig nøyaktig ved hjelp av en datamaskin.

Kommentarer (3)
skrev Audun Ingebrigtsen
svarte Erik Dyrhaug
skrev Stian Jørgensrud
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.