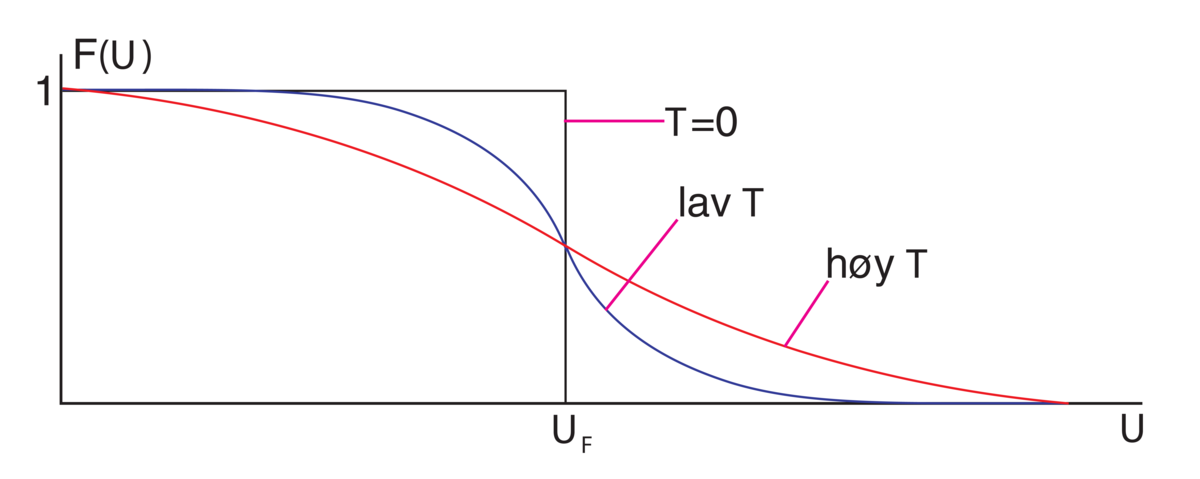
Fermi-Dirac-statistikk er en kvantemekanisk beskrivelse av energifordelingen til fermioner som protoner og nøytroner.
Faktaboks
- Uttale
- fˈermi-dirˈac-statistikk
- Etymologi
-
oppkalt etter fysikerne Enrico Fermi og Paul A. M. Dirac
Kjennskapet til Fermi-Dirac-statistikk har vært av grunnleggende betydning for flere ulike deler av fysikken, slik som forståelsen av metallers elektriske og termiske ledningsevne, for elektronemisjon og for studier av strukturene til atomer og molekyler.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.