Spinn brukes i fysikken som regel i følgende to betydninger:
- En generell dreieimpuls
- En intern kvantemekanisk dreieimpuls til partikler, som elektronspinn
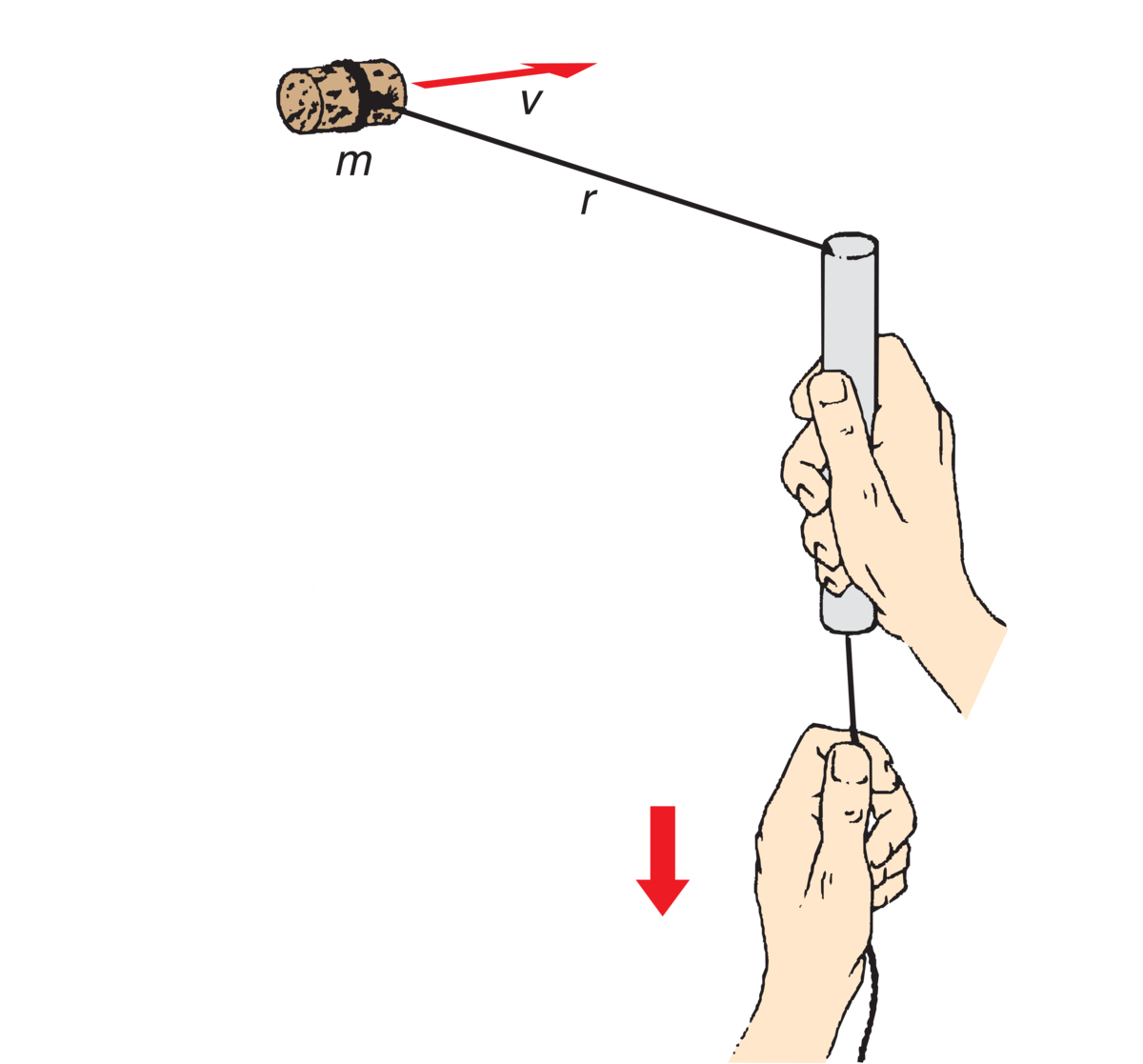
Illustrasjon av spinn. Når et legeme roterer fritt i en sentralbevegelse, er legemets spinn en bevegelseskonstant. Figuren viser en kork som er festet til en sterk tråd og brakt i rotasjon i horisontalplanet. Korkens spinn L (også kalt dreieimpuls) er lik produktet av dens masse m, dens fart v, og radien r, det vil si S = m · r · v.
Fører vi inn omløpstiden T, blir S proporsjonal med r2/T. Holder vi nå røret i ro mens korken roterer med forholdsvis lang snor og så korter inn radien r ved å trekke i snoren, må også omløpstiden T minke fordi spinnet S skal holdes uforandret. Korken vil derfor gå stadig fortere rundt jo mer den nærmer seg sentrum.
Samme prinsipp utnyttes av for eksempel kunstløpere når de dreier seg rundt på én skøyte (piruett). Løperen starter den roterende bevegelsen med utstrakte armer og legger så armene inntil kroppen for å få en hurtigere rotasjon.
Spinn brukes i fysikken som regel i følgende to betydninger:
Spinnet av en partikkel (et bevegelig massepunkt) omkring et fast punkt er lik produktet av avstanden fra det faste punktet til partikkelen (radiusvektoren) og komponenten av partikkelens bevegelsesmengde (impuls) vinkelrett på radiusvektoren. Ved sentralbevegelse er spinnet en bevegelseskonstant.
Spinnet av et stivt legeme omkring en akse er lik produktet av legemets vinkelhastighet og dets treghetsmoment om aksen.
For et legeme som roterer fritt, kan spinnet om et punkt beskrives matematisk av en vektor. I spesialtilfellet hvor legemet er en punktpartikkel, vil retningen til denne vektoren stå vinkelrett på planet som partikkelen roterer i.
I alminnelighet roterer ikke legemet om en hovedtreghetsakse. Spinnretningen faller da ikke sammen med den momentane rotasjonsakse (se under rotasjon).
Hvis det ikke virker noe kraftmoment på legemet, er legemets spinn en bevegelseskonstant, spinnretningen er fast i rommet, og den momentane rotasjonsaksen roterer omkring spinnaksen, nutasjon.
En av de grunnleggende bevaringslovene i mekanikken fastslår at spinnet for et isolert system holder seg konstant, og at det må utsettes for et ytre kraftmoment for at spinnets verdi eller retning skal endres.
Spinn kan i kvantemekanikken brukes i samme betydning som i den klassiske mekanikken, men opptrer her som en kvantisert størrelse. Innen kvantemekanikk er det dessuten vanlig at begrepet spinn er forbeholdt den interne dreieimpulsen til en partikkel, i motsetning til den totale dreieimpulsen.
Kvadratet av spinnvektoren for et atomært system (atom, molekyl, atomkjerne) i en egentilstand er lik J (J + 1)ℏ2, hvor ℏ = h/2π, h er Plancks konstant. J er et tall, spinnkvantetallet. Det kan anta verdiene 0, 1, 2, 3,..., heltallig spinn; eller ½, 3/2, 5/2,..., halvtallig spinn.
Etter kvantemekanikkens lover er spinnet, som i den klassiske mekanikk, en bevegelseskonstant så lenge et system har rotasjonssymmetri. Lengden av en spinnkomponent som observeres langs en akse er lik Mℏ, hvor M er et tall mellom –J og +J, heltallig hvis J er heltallig, og halvtallig hvis J er halvtallig. Spinnkomponenten observeres som regel i forhold til retningen av et magnetfelt, og M kalles derfor magnetisk kvantetall.
Et systems totale spinn fremkommer ved bidrag fra de enkelte partiklers spinn. For hver partikkel i systemet er spinnet satt sammen av banespinnet, det vil si bevegelsesmengdemomentet om systemets tyngdepunkt, og egenspinnet. På samme måte som systemets totale spinn uttrykkes ved kvantetallet J, uttrykkes den enkelte partikkels spinn ved kvantetallene for totalt spinn, j, for banespinn, l, og for egenspinn, s. Av disse er l alltid et helt tall.
For partikler som inngår i atomære systemer (elektron, proton, nøytron), er s = ½ og j = l ± ½. For andre elementærpartikler kan egenspinnet være heltallig eller halvtallig. Partikler med heltallig egenspinn kalles bosoner, partikler med halvtallig egenspinn kalles fermioner.

Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.