En matematisk funksjon kan tenkes på som en boks der man putter inn såkalte variable, og hvor det kommer funksjonsverdier ut av boksen. De variable kalles argumentene til funksjonene.
Det enkleste tilfellet er at man beskriver kurver i et plan. Dersom man legger inn et kartesisk koordinatsystem i planet med koordinater x og y, skrives funksjonen y = f(x). Den variable x er funksjonens argument, og y er funksjonsverdien. Her angir x posisjonen langs x-aksen og y posisjonen langs y-aksen. Funksjonen kan også inneholde størrelser (se eksempler nedenfor) som ikke er med blant argumentene, men som er med på å definere hva slags kurve det matematiske uttrykket beskriver. Slike størrelser kalles parametre og angir ikke posisjon i xy-planet.
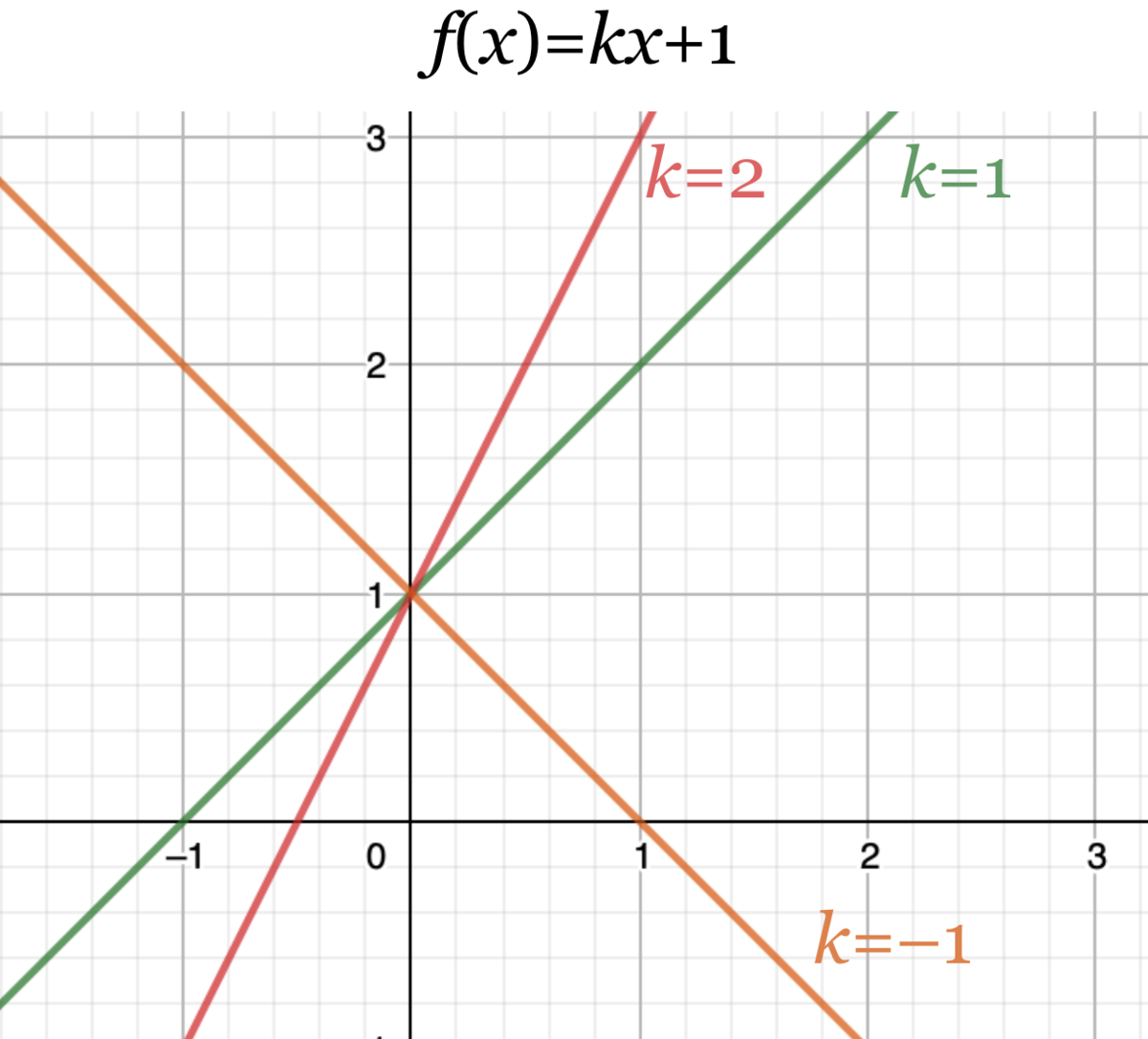
Eksempel 1: Ligningen y = kx + 1 vil alltid gi en rett linje som vil gå gjennom punktet (0,1), men ulike verdier som velges for k vil gi ulike linjer (linjer med ulike stigningstall, se figuren). Her er k en parameter som bestemmer hvor bratt linjen er.
Eksempel 2: Et annengradsuttrykk y = f(x) = ax2+bx+c kan beskrive sirkler, ellipser, parabler og hyperbler. Verdiene av parametrene a, b og c bestemmer hva slags kurve det matematiske uttrykket beskriver, mens argumentet x angir verdien langs x-aksen for ulike punkter på den aktuelle kurven. Funksjonsverdien y angir verdier langs y-aksen for punktene på kurven.
En kurves ligning er gitt på parameterform hvis koordinatene x og y er gitt som funksjon av en hjelpevariabel kalt parameteren.
Eksempel 3: Det grafiske bildet av x = a·sin t, y = b·cos t er en ellipse når parameteren t varierer. Vi sier at ellipsens ligning er gitt på parameterform.
Hvis vi skal beskrive en flate i rommet, kan vi innføre et kartesisk koordinatsystem med tre koordinater, x og y som beskriver posisjonen i xy-planet av et punkt på flaten, og z som beskriver hvor høyt over xy-planet punktet er. Denne høyden avhenger av posisjonen i xy-planet, det vil si at z er en funksjon av x og y, som skrives z = f(x,y). Likningen til slike flater kan også gis på parameterform som vi skal se i neste eksempel.
Eksempel 4: Vi skal nå beskrive en kuleflate. Da vil det forenkle beskrivelsen å innføre såkalte kulekoordinater, r, θ og φ , der koordinaten r angir avstanden fra origo til et punkt i rommet, og vinkelkoordinatene θ og φ forteller hvilken retning en linje fra origo til punktet har. Anta kulen har radius R. Vi lar det kartesiske koordinatsystemet og kulekoordinatsystemet ha samme origo, og plasserer kuleflaten med sentrum i origo. Da forenkles likningen for kuleflaten i kulekoordinatene til r = R. Hvis en er interessert i x, y og z -koordinatene på kuleflaten, finnes de av parameterformen for kuleflatens likning x = R cos θ sin φ, y = R sin θ sin φ og z = R cos φ, der θ og φ opptrer som parametre.


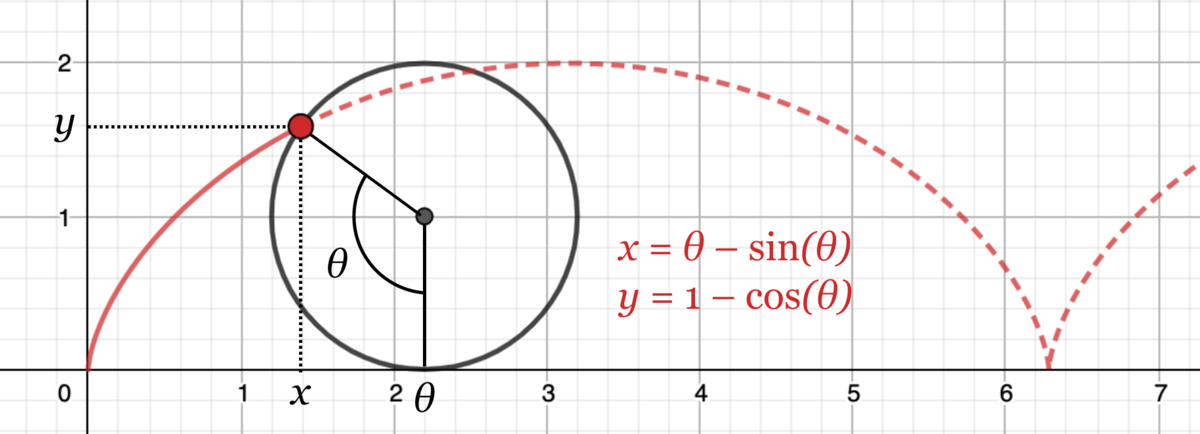


Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.