areal – Store norske leksikon

Areal er en matematisk betegnelse som angir hvor stor en flate er. Areal kalles også flateinnhold. Areal måles i arealenheter som kvadratmeter, mål og dekar.

Faktaboks

Også kjent som: flateinnhold

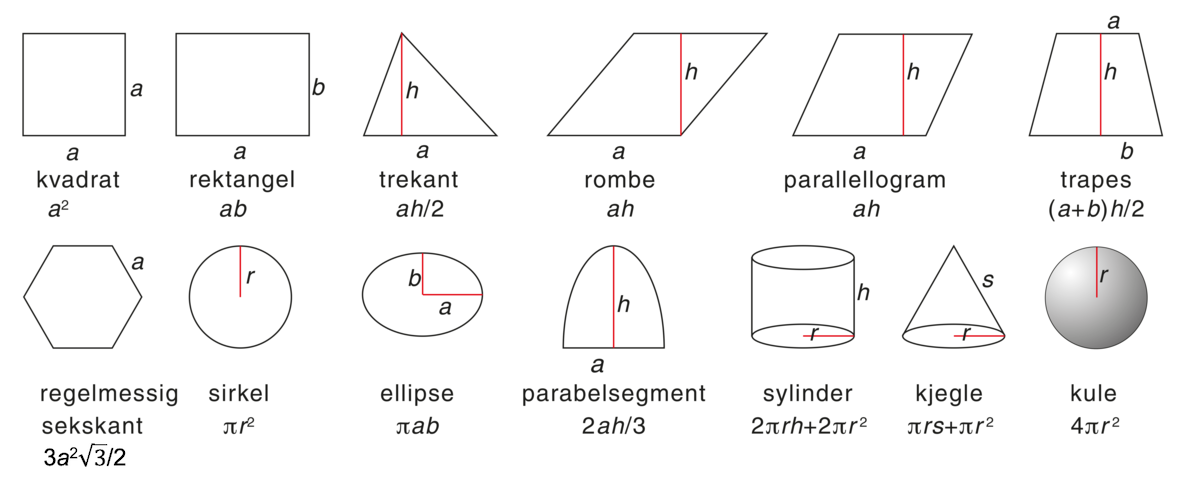
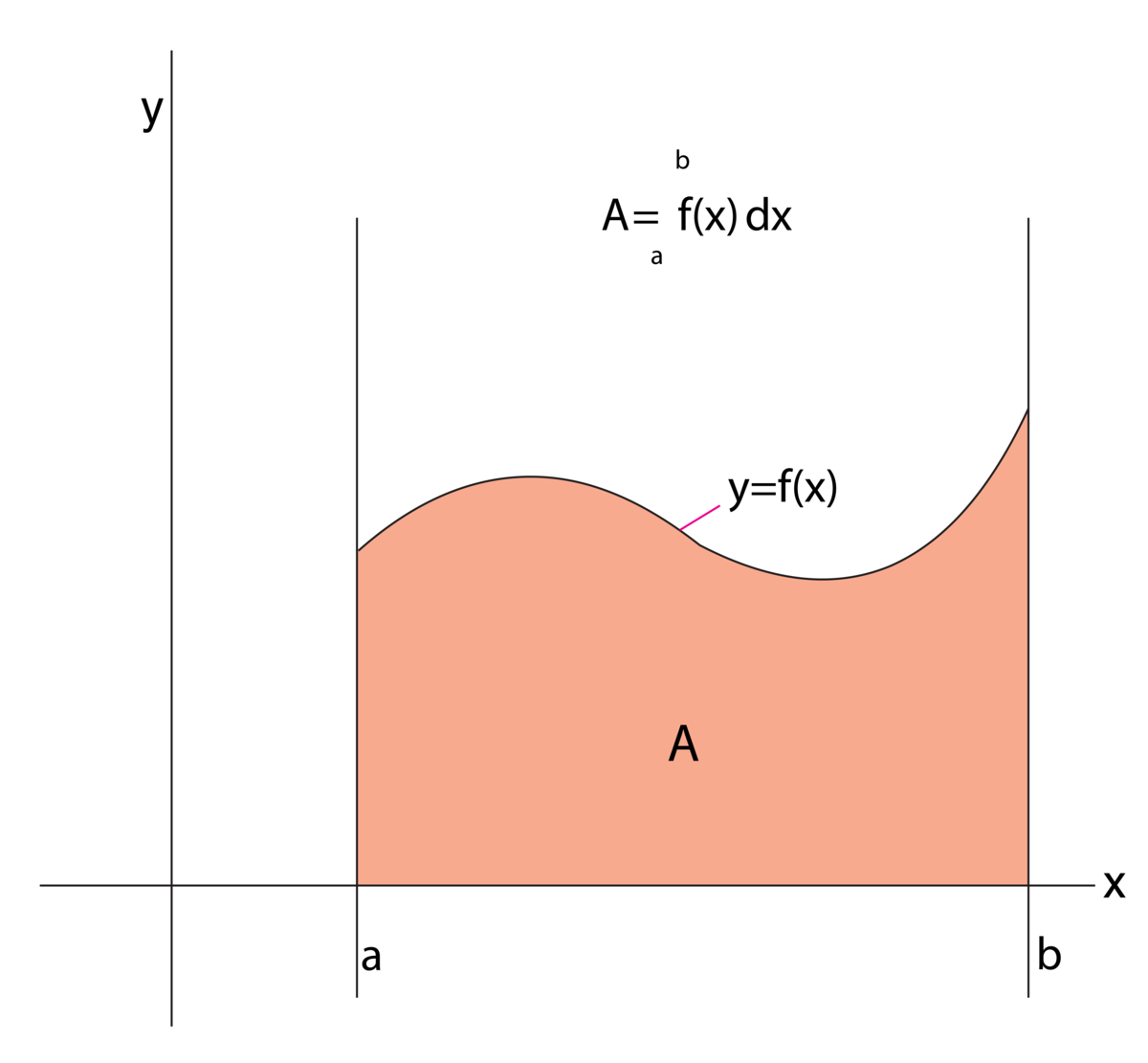
Arealet til et plant flatestykke er vanligvis definert som det antallet flateenheter det inneholder. Hvis et flatestykke for eksempel inneholder tre kvadratmeter, sier man at arealet til flatestykket er tre kvadratmeter.

Formler for areal

Formler for arealet til noen plane figurer, og for overflatearealet til noen tredimensjonale legemer:

Kvadrat med sidekant a: \(a^2 \)
Rektangel med sidekanter a og b: \(ab \)
Trekant med grunnlinje a og høyde h: \(\frac{ah}{\mathrm{2} } \)
Rombe med grunnlinje a og høyde h: \(ah \)
Parallellogram med grunnlinje a og høyde h: \(ah \)
Trapes med parallelle sider a og b, og høyde h mellom dem: \(\frac{{(a+b)\cdot h} }{\mathrm{2} }\)
Regelmessig sekskant med sidekanter a: \(3 \cdot a^2 \sqrt{\frac{\mathrm{3} }{\mathrm{2} }}\)
Sirkel med radius r: \(\pi\cdot r^2\)
Ellipse med halvakser a og b: \(\pi\cdot ab\)
Parabelsegment med bredde a og høyde h: \(\frac{{2ah} }{\mathrm{3} } \)
Sirkulær sylinder med radius r og høyde h: \(2\pi\cdot rh+2\pi\cdot r^2\)
Sirkulær kjegle med radius r og høyde h: \(\pi\cdot rs+\pi\cdot r^2\)
Kuleflate med radius r: \(4\pi\cdot r^2\)

Beregning av areal

Areal av mangekanter

I alminnelig geometri blir arealet av en mangekant bestemt ut fra følgende tre forutsetninger:

1) Et kvadrat med lengdeenheten til side har et areal som er lik 1 flateenhet. For eksempel har et kvadrat med 1 meter lange sider et areal på 1 kvadratmeter.

2) Kongruente flatestykker har samme areal.

3) Arealet av et plant flatestykke som er sammensatt av flere andre, er summen av delenes areal.

Dersom en figur er begrenset av rette linjer, beregnes arealet ofte ved at figuren oppdeles i trekanter, og så beregnes arealet av trekantene hver for seg. Dette kalles triangulering. Når figuren ikke har en rettlinjet begrensning, tilnærmer man den med mangekanter og bruker samme fremgangsmåte.

Integrasjon

Matematisk svarer beregning av areal til integrasjon. Det arealet som begrenses ved x-aksen, de to loddrette linjene x = a og x = b og kurven y = f(x), er gitt ved det bestemte integralet

\[A=\int\limits_a^b f(x) \, \mathrm{d}x\]

For en krum flate kan arealet defineres og beregnes som grenseverdien for overflaten av et omskrevet polyeder. Det kan også finnes ved integrasjon.

Planimeter

Når en figur er tegnet på papir, som for eksempel på et kart, kan arealet måles direkte hjelp av et planimeter. Man følger konturen av en lukket kurve med planimeterets spiss, og arealet kan avleses på et målehjul.

Les mer i Store norske leksikon

Kommentarer

Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.

Du må være logget inn for å kommentere.

Fagansvarlig for Algebraisk geometri

Jon Eivind Vatne

førsteamanuensis, Handelshøyskolen BI