Mengdelære er en gren av matematikken hvor begrepet mengde har en sentral plass. En mengde i denne sammenhengen er en samling objekter som kalles elementer. Vanligvis er elementene tall, symboler for tall, funksjoner, punkter eller linjer. Elementene kan også selv være mengder. Det er ikke noe krav at alle elementene i en mengde må være av samme slag.
Faktaboks
- Også kjent som
-
engelsk: set theory
En mengde kan være endelig eller uendelig. Mengden av alle naturlige tall er et eksempel på en uendelig mengde, mens mengden av alle naturlige tall fra 1 til 10 er en endelig mengde.
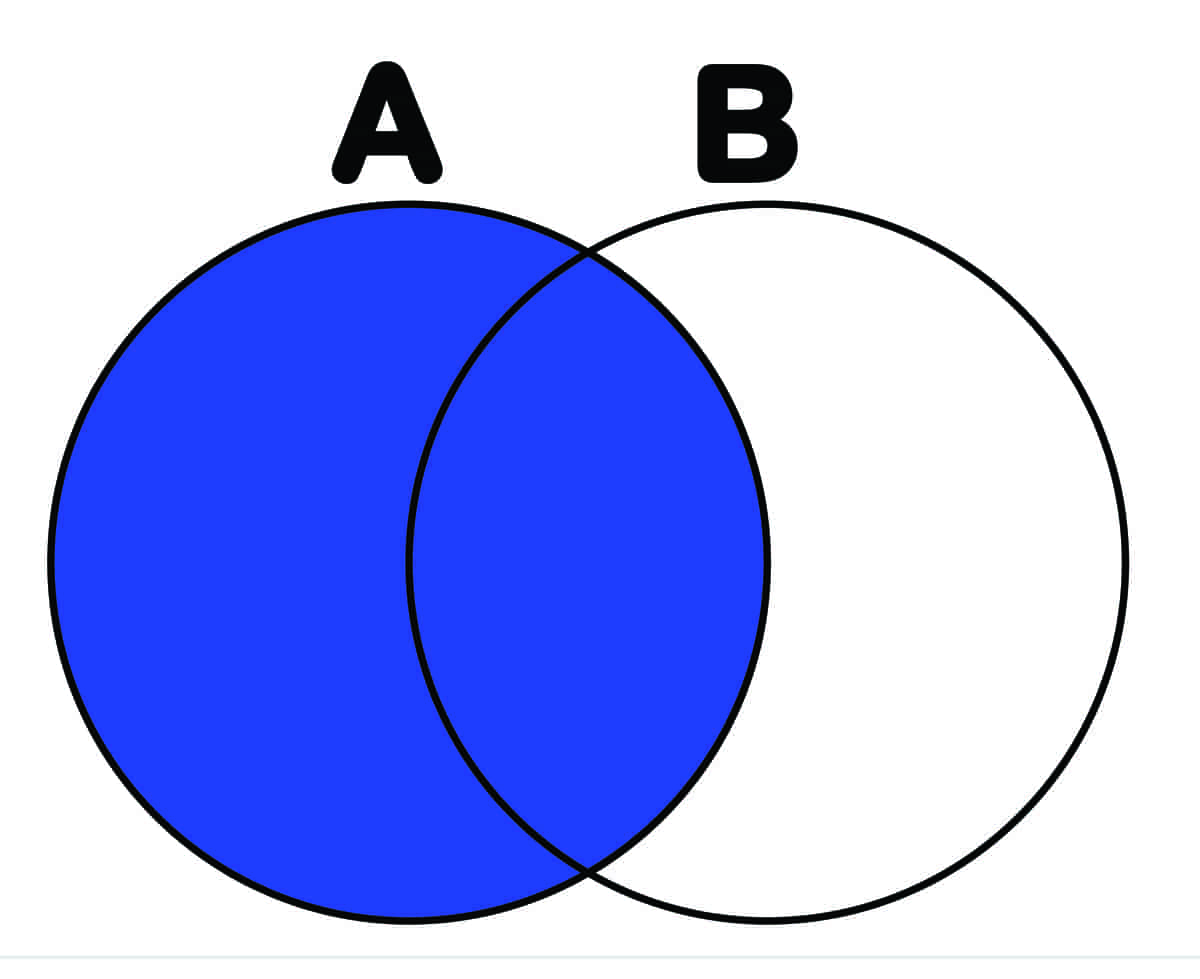
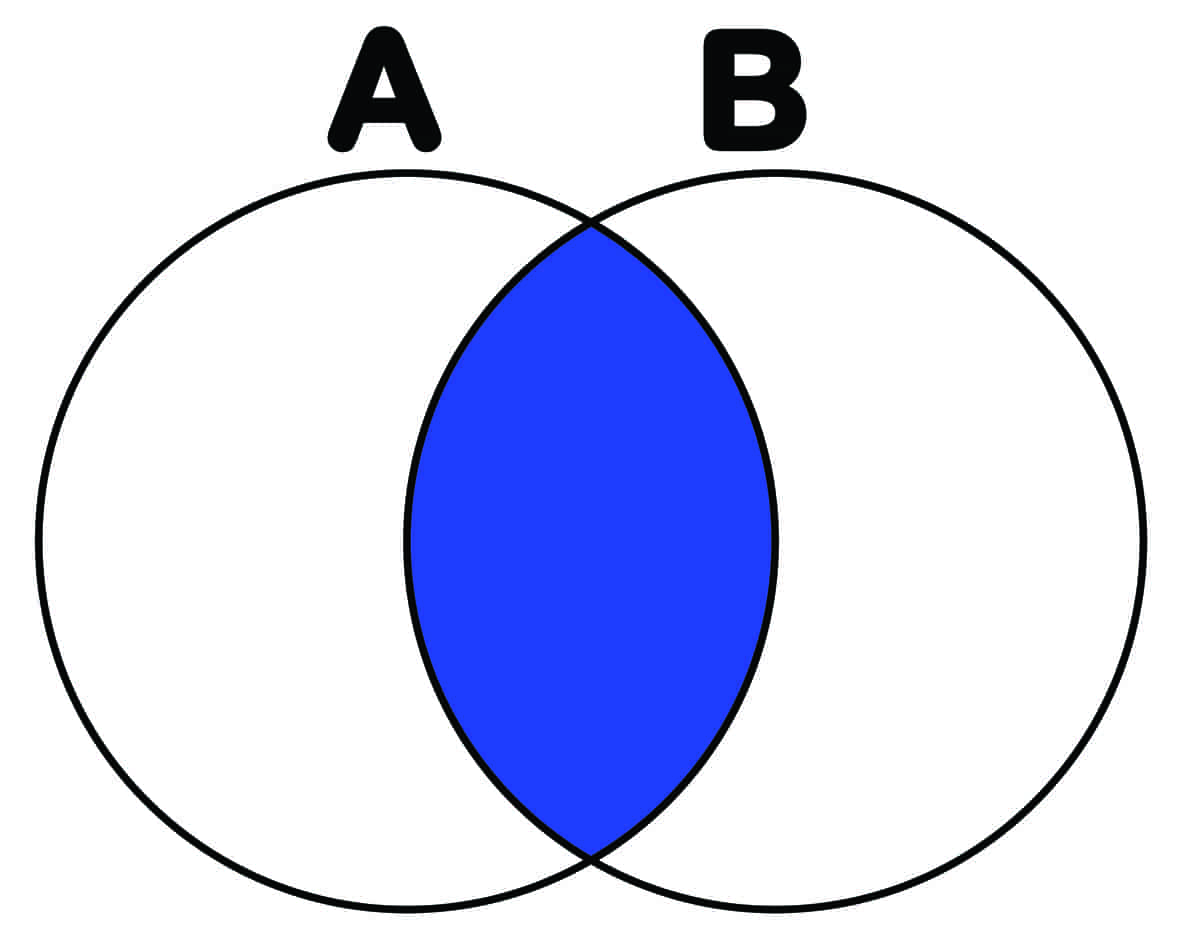
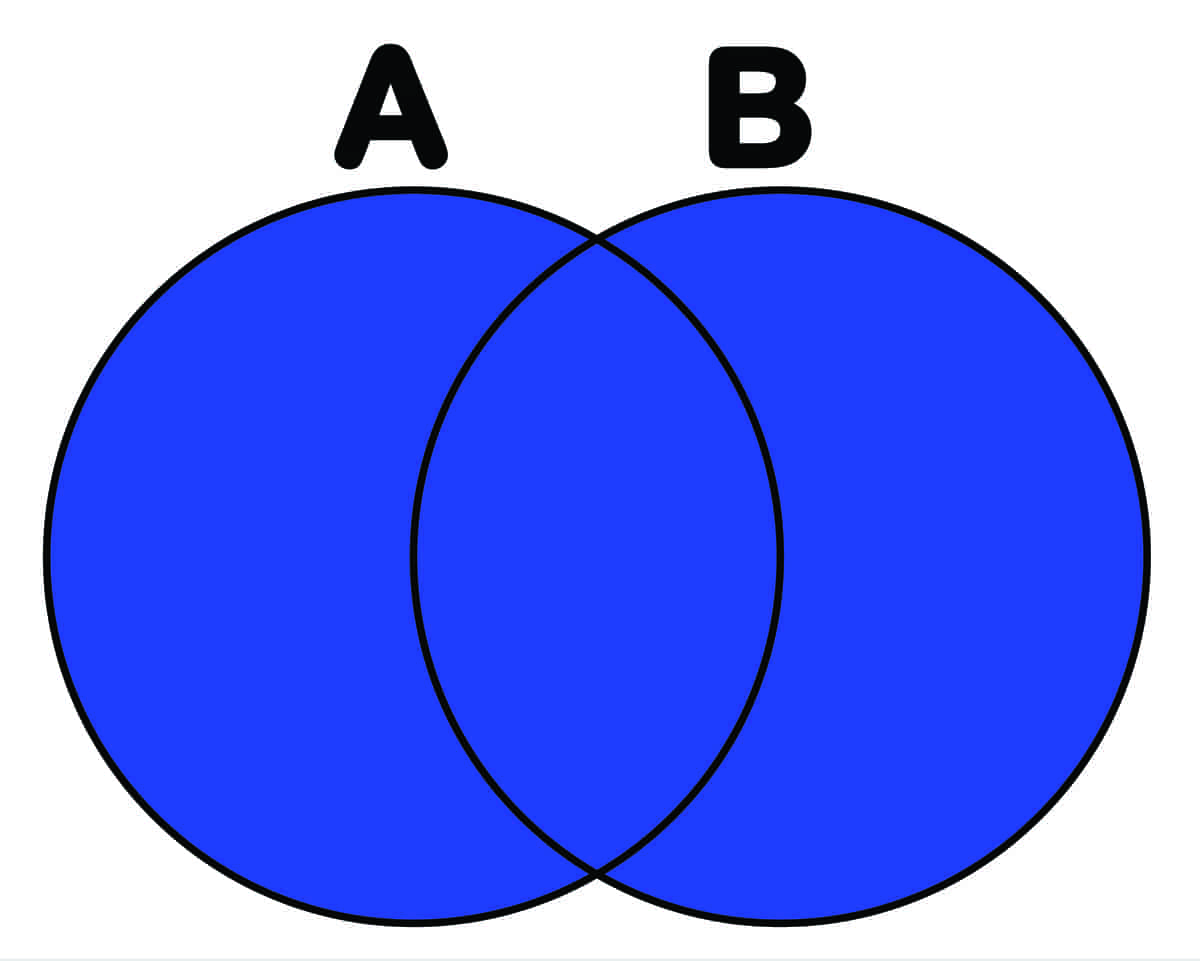
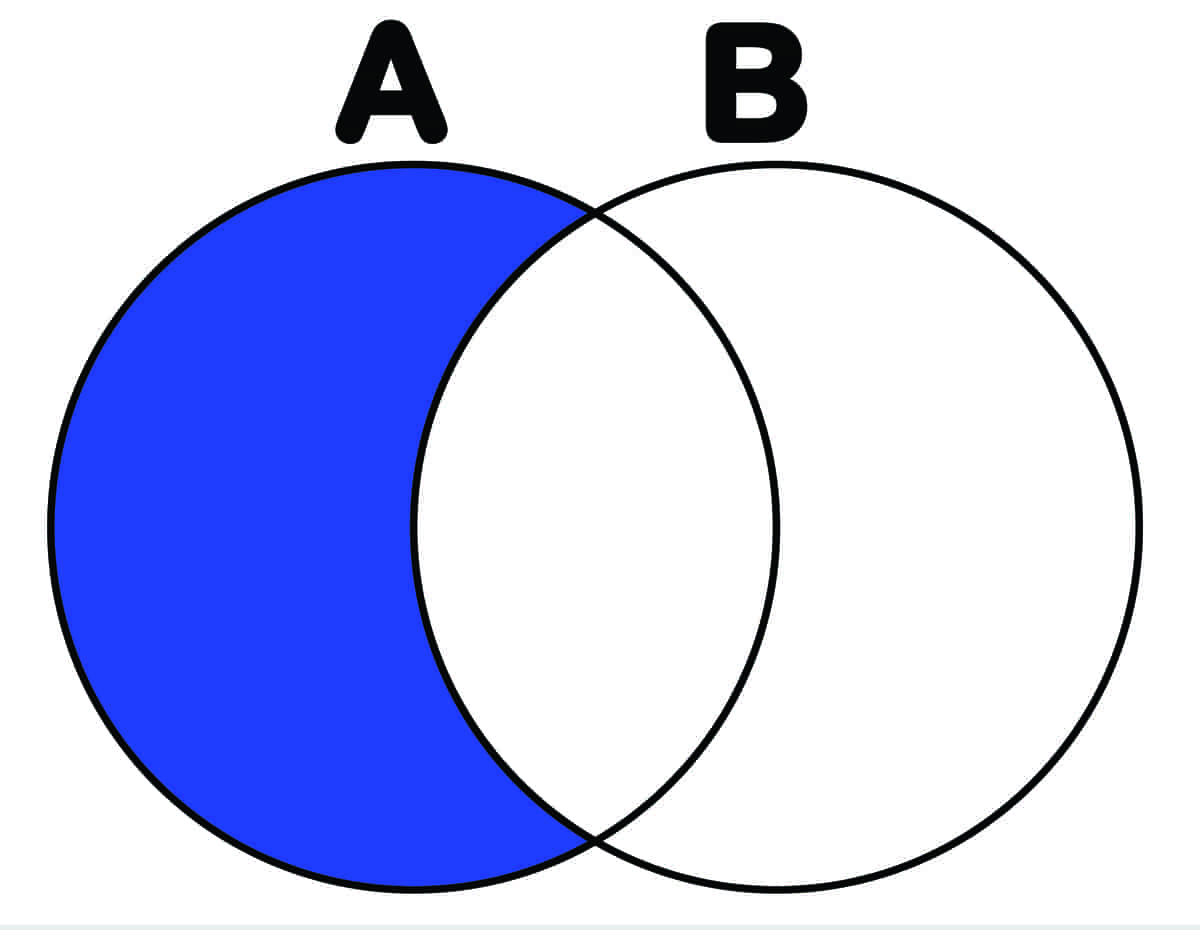
Mengdelæren ble grunnlagt av den tyske matematikeren Georg Cantor. Hans ideer brakte nye synsmåter inn i mange matematiske problemer, og mengdelæren har fått stor betydning på en rekke områder innen matematikken. En god del av det matematikken dreier seg om kan oppfattes som mengder og relasjoner mellom mengder.





Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.