Reynolds' tall brukes i fysikk og kjemi til å beskrive strømningen i en væske eller en gass. Det er oppkalt etter Osborne Reynolds.
Faktaboks
- Uttale
- rˈenəldz –
- Etymologi
-
etter Osborne Reynolds
Reynolds' tall brukes i fysikk og kjemi til å beskrive strømningen i en væske eller en gass. Det er oppkalt etter Osborne Reynolds.
etter Osborne Reynolds
Hver del i en viskøs væske eller gass vekselvirker med sine nærmeste naboer, slik at det oppstår en friksjonskraft mellom dem. Videre vil hver del av en væske eller gass ha en bestemt hastighet og massetetthet, noe som gir den en bevegelsesmengde. Jo større hastighet og massetetthet, jo større er bevegelsesmengden, og jo større treghet sier vi at væsken eller gassen har. De kreftene som motsetter seg forandringer i bevegelsesmengden til væsken eller gassen kalles ofte treghetskrefter. Reynolds' tall er forholdet mellom treghetskrefter og friksjonskrefter i en væske eller gass. Alternativt kan Reynolds’ tall også uttrykkes som forholdet mellom den kinetiske energien og friksjonsarbeidet som blir gjort inne i væsken eller gassen.
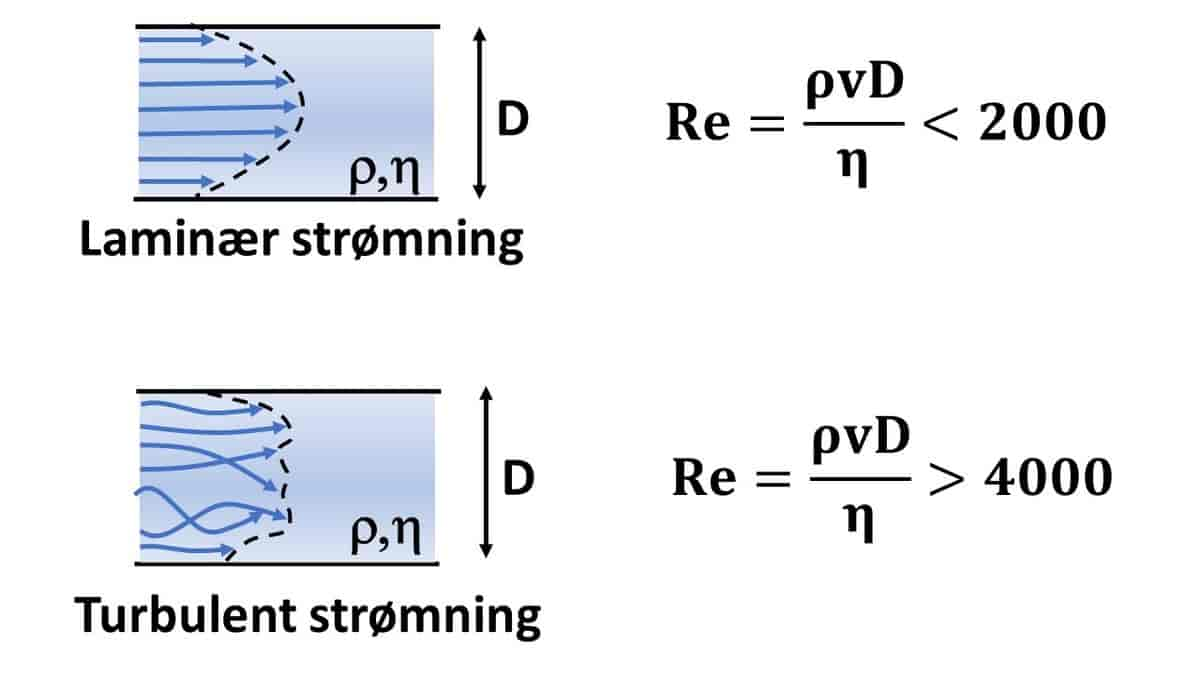
Dersom en væske med massetetthet ρ og viskositet η strømmer med gjennomsnittsfart v gjennom et rør med diameter D, kan man skrive Reynolds’ tall som
\[Re = \frac{\rho VD}{\eta}\]
En praktisk og mye brukt regel basert på Reynolds' opprinnelige observasjoner er at når Reynolds tall er mindre enn 2000, vil væskestrømmen ofte være laminær slik at volumstrømmen kan uttrykkes ved Poiseuilles lov. Dersom hastigheten økes, vil man observere en overgang fra laminær til turbulent strømning, og dette inntreffer ofte ved den kritiske hastigheten for verdier av Reynoldstallet mellom 2000 og 4000. I turbulent strømning vil hastighetsprofilen til væskestrømmen være noe tilfeldig fordelt inne i røret, men ofte observeres å være flatere enn ved laminær strøm.
I andre geometrier inntreffer overgangen fra laminær til turbulent strømning ved andre Reynoldstall. Forstyrrelser i væskestrømmen har en god del å si for ved hvilket Reynoldstall overgangen fra laminær til turbulent strøm inntreffer. Slike forstyrrelser kan være vibrasjoner, krefter som virker på tvers av strømningsretningen, eller geometrier som påvirker strømningsretningen. På 1960-tallet ble det gjort forsøk med svært lange rør montert i bomberom for å fjerne mest mulig forstyrrelser, og det viste seg da at væskestrømmen kunne forbli laminær for Reynoldstall over 100 000! I senere tid har man gjort nye forsøk med frie og vertikale jetstrømmer, og funnet at laminær strømning ved enda større Reynoldstall er mulig. Man har enda ikke funnet en øvre grense for Reynoldstallet ved laminær strøm, men man vet at jo mindre påvirket systemet er av fluktuasjoner, jo større kan Reynoldstallet være ved laminær strøm.
Reynolds’ tall er viktig for å kunne si noe om når turbulens kan forventes å oppstå og om viskøse krefter eller treghetskrefter spiller den viktigste rollen. Store rør og store objekter som beveger seg i væsker vil generelt gi store Reynoldstall. For strømning av små objekter i væsker, slik som blodceller i kapillarer, vil størrelsen være så liten at Reynoldstallet også er svært lite. Dette betyr at friksjonskrefter spiller en viktig rolle på liten skala, og man vil sjelden observere turbulens. Kjennskap til Reynolds' tall er også viktig når man skal overføre resultater som er oppnådd ved forsøk med små modeller til modeller i full størrelse. Det gjelder for eksempel når man skal bruke resultater fra modeller i vindtunnel på fly i full målestokk.

Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.