Normalfordeling er en sannsynlighetsfordeling som blir mye brukt i matematisk statistikk. Grunnen er dels at visse typer av observerte data er tilnærmet normalfordelt, og dels at normalfordelingen opptrer som grensefordeling for en rekke andre typer fordelinger.
Faktaboks
- Uttale
- normˈalfordeling
- Også kjent som
- Gauss–Laplaceske fordeling
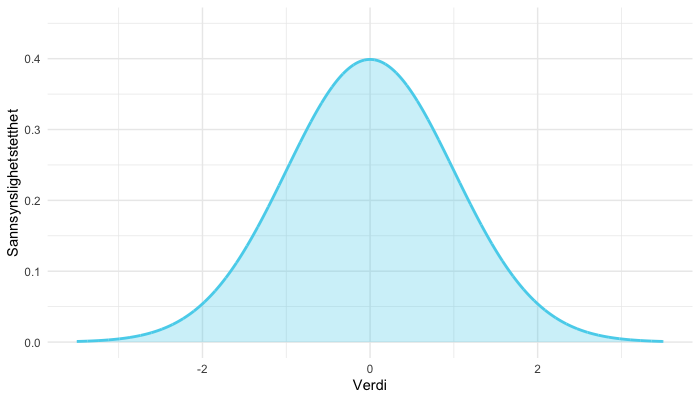
Normalfordelingskurven kalles også Gauss-kurve, etter den tyske matematikeren Carl Friedrich Gauss.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.