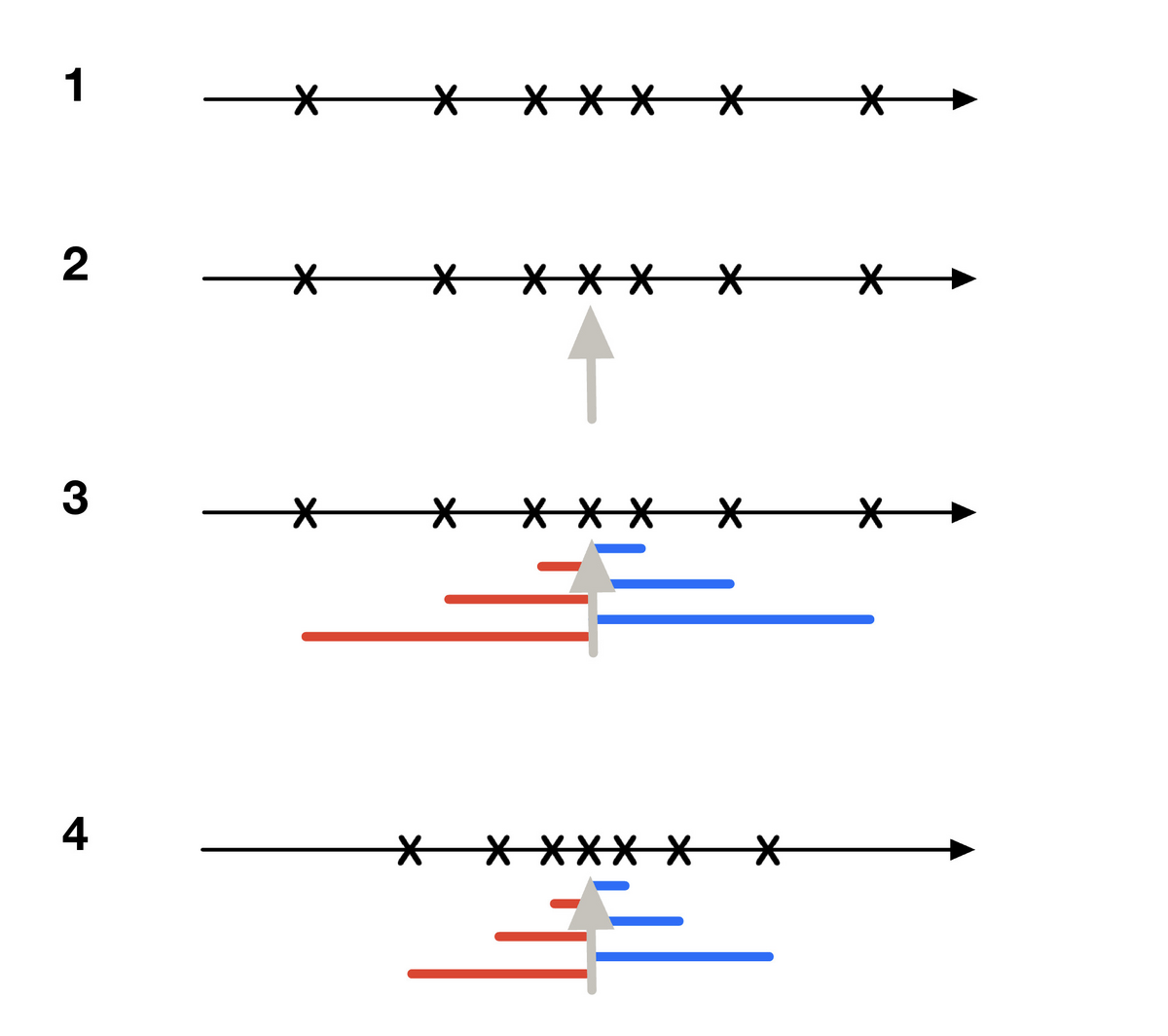
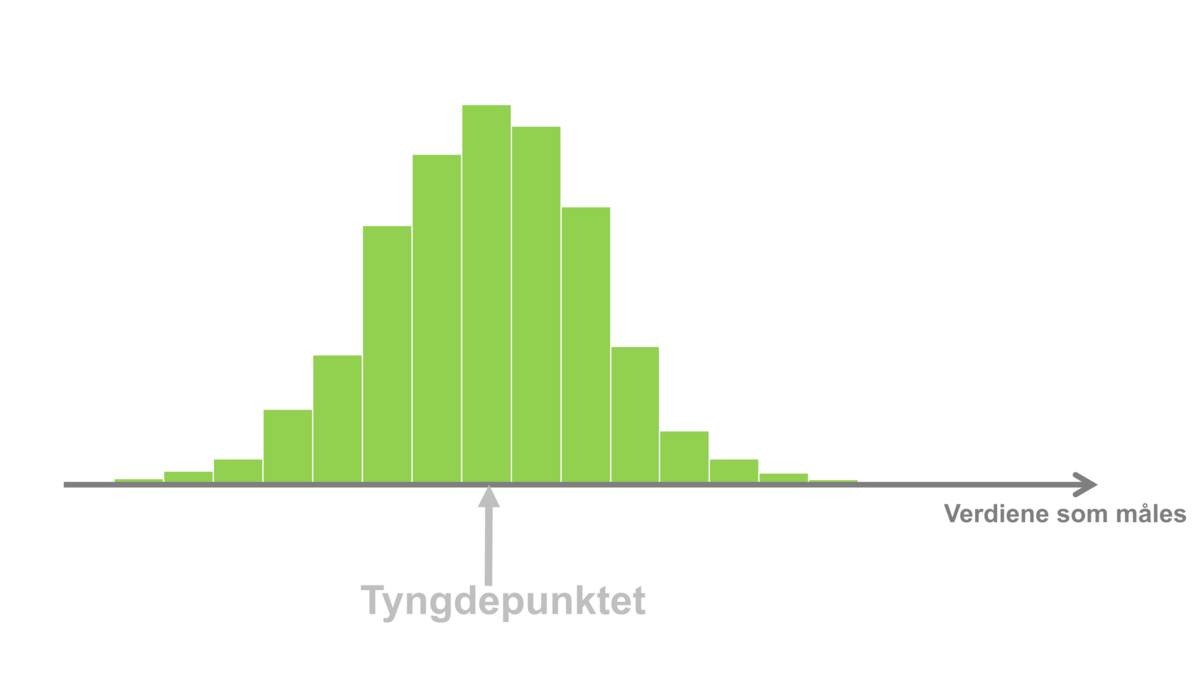
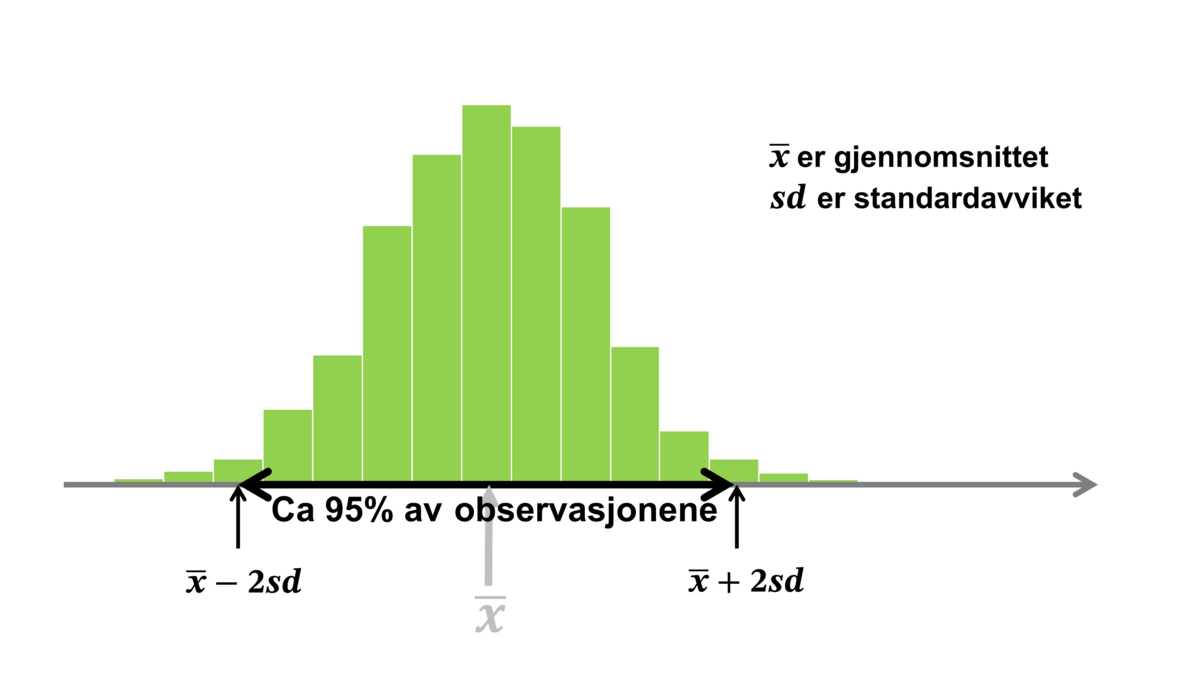
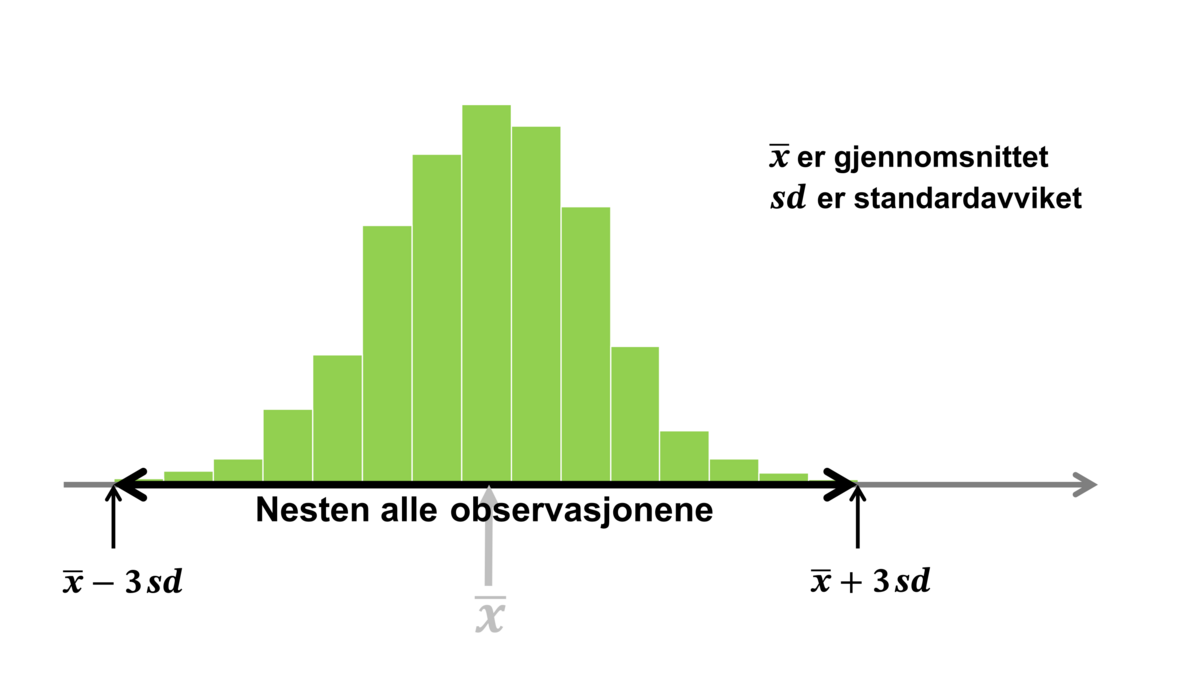
Et standardavvik er i statistikk et tall som oppsummerer variasjonen i en samling tallverdier. Standardavviket sier noe om hvor spredt verdiene er, og kalles derfor ofte et spredningsmål.
Det finnes både observerbart standardavvik og teoretisk standardavvik. Det observerbare standardavviket er et tall som beskriver variasjonen eller spredningen i et innsamlet tallmateriale. Det er oftest dette som menes når man snakker om standardavvik.
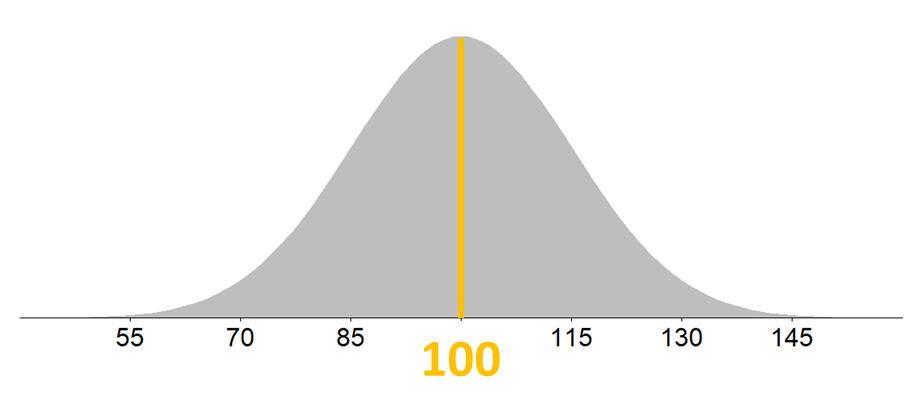
Det teoretiske standardavviket spesifiserer variasjonen i en statistisk modell, for eksempel i normalfordelingen.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.