Den assosiative lov er en matematisk lov som blant annet gjelder for addisjon og multiplikasjon.
Faktaboks
- Uttale
- assˈosiative lov
- Etymologi
-
til assosiasjon
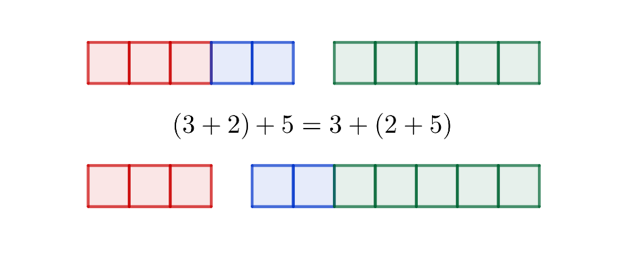
For addisjon sier loven at når tre tall adderes, blir det samme resultat enten summen av de to første tallene adderes til det tredje tallet, eller det første tallet adderes til summen av de to siste. Med symboler kan dette skrives
a + b + c = (a + b) + c = a + (b + c)
der a, b og c er reelle tall.
For multiplikasjon sier loven at når tre tall multipliseres, blir det samme resultat om man først multipliserer de to første og deretter det tredje tallet med dette, eller om man multipliserer de to siste tallene og så multipliserer det første tallet med dette. Dette kan skrives
a· b · c = (a · b) · c = a · (b · c)




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.