kinetisk energi – Store norske leksikon

Figur 1. Pendel med veksling mellom stillingsenergi og kinetisk energi

Pendel

Av Jostein Riiser Kristiansen.

Lisens: Begrenset gjenbruk

Figur 2. Den røde grafen viser hvordan et legemes relativistiske kinetiske energi avhenger av dets hastighet, og den grønne hvordan den klassiske kinetiske energien avhenger av hastigheten. Den relativistiske sammenhengen er korrekt for alle hastigheter opp til lyshastigheten, mens den klassiske bare kan brukes når legemets hastighet er mye mindre enn lyshastigheten.

Energigraf

Av Jostein Riiser Kristiansen.

Lisens: CC BY SA 3.0

Kinetisk energi, også kalt bevegelsesenergi, er den energien en gjenstand har på grunn av hastigheten sin. Denne energien er lik det arbeidet som må gjøres for å akselerere legemet fra ro til den farten det har. Et legeme i ro har ingen kinetisk energi.

Faktaboks

Også kjent som: bevegelsesenergi

Symbolet for energi er E. For å gjøre det klart at det er kinetisk energi, skriver man gjerne E_kin .

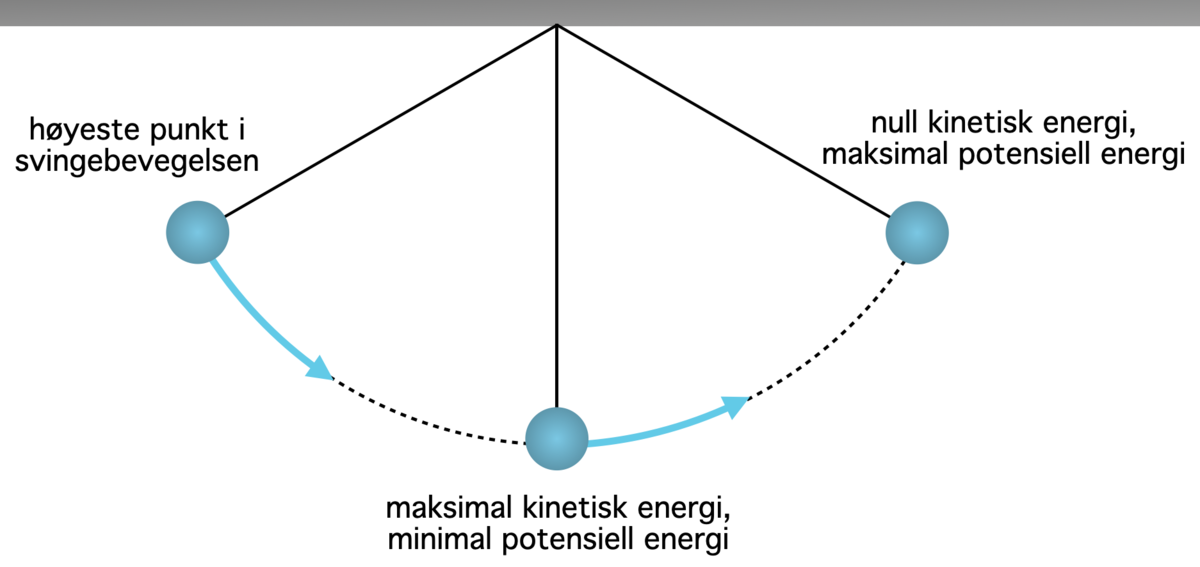
Eksempel: I en pendel veksler energien mellom potensiell energi (stillingsenergi) og kinetisk energi. Den kinetiske energien er null i ytterstillingen, og maksimal når pendelen passerer likevektsposisjonen. Se figur 1.

Et legemes bevegelsesenergi kan omdannes til andre typer energi. Når en gjenstand for eksempel kastes oppover i et tyngdefelt og bremser ned, omdannes den kinetiske energien til potensiell energi.

Kinetisk energi i forhold til hastighet

Klassisk uttrykk

For alminnelige hastigheter (det vil si hastigheter som er mye mindre enn lyshastigheten), kan den kinetiske energien uttrykkes som

E = ½ mv²

Her er m massen til legemet og v er hastigheten. Dette kalles det klassiske uttrykket for kinetisk energi. Den kinetiske energien til et legeme i bevegelse er altså proporsjonal med kvadratet av hastigheten.

Relativistisk uttrykk

Ifølge relativitetsteorien er den kinetiske energien lik

\[E = m_0c^2 \cdot \left(\frac{1}{ \sqrt{1 – \frac{v^2}{c^2} } }− 1\right)\]

der m₀ er legemets masse når det er i ro (hvilemassen), v er hastigheten og c er lyshastigheten. Dette er det relativistiske uttrykket for kinetisk energi. Det viser at når farten nærmer seg lyshastigheten, går den kinetiske energien mot uendelig. Dette innebærer at det ikke er mulig å akselerere et legeme fra en lavere hastighet enn lyshastigheten til overlyshastighet.

Figur 2 viser hvordan den relativistiske kinetiske energien og den klassiske avhenger av hastigheten.

Rotasjonsenergi og kinetisk energi

Når et legeme roterer med treghetsmoment I og vinkelhastighet ω, er den kinetiske energien

E = ½ Iω²

Dette betyr at jo fortere et legeme roterer, desto større kinetisk energi, i form av rotasjonsenergi, har det.

Les mer i Store norske leksikon

Kommentarer

Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.

Du må være logget inn for å kommentere.

Fagansvarlig for Mekanikk

Jostein Riiser Kristiansen