pendel (fysikk)
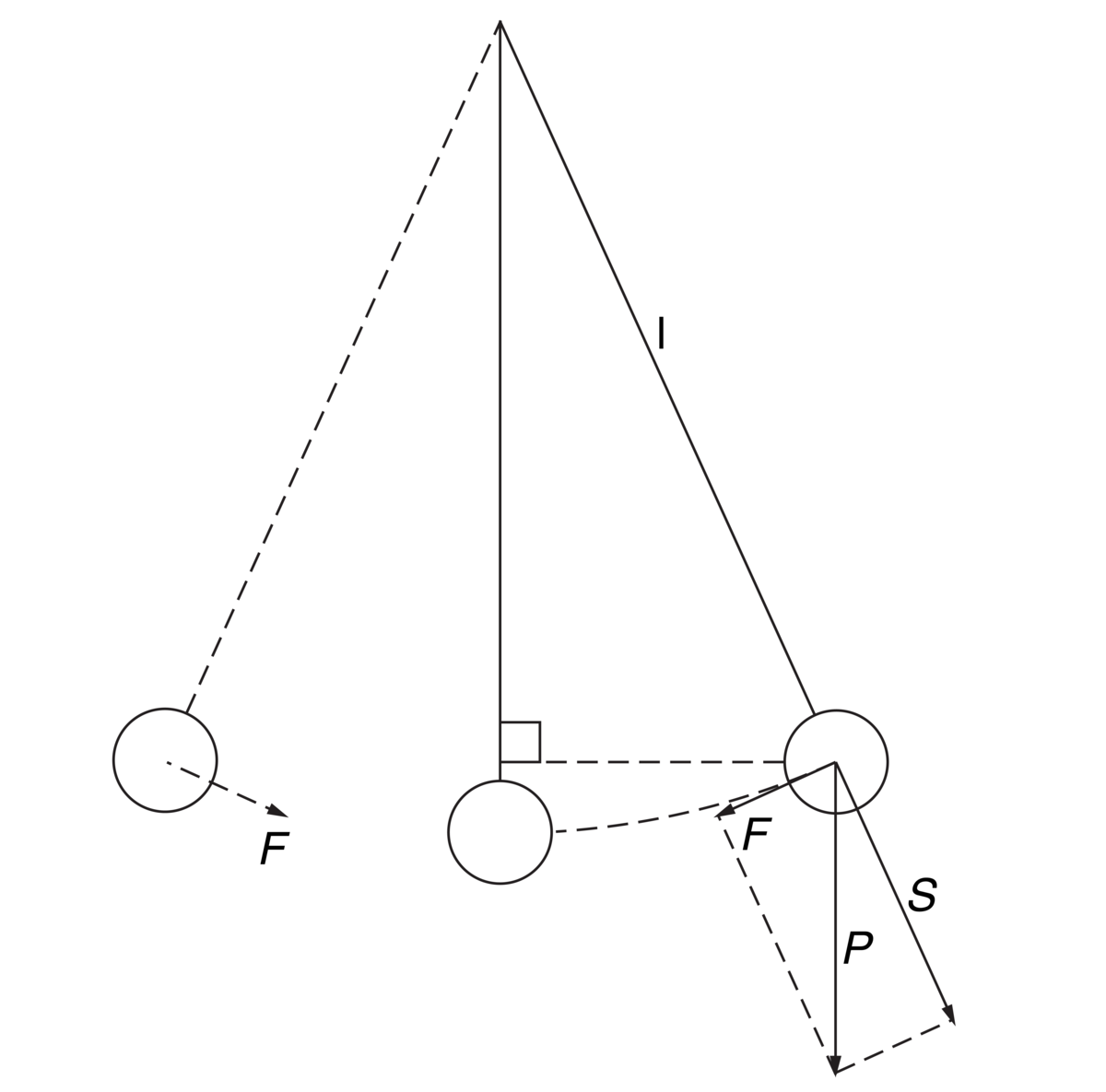
Pendel. Tyngden P av loddet (massepunktet) i en matematisk pendel kan tenkes erstattet av en kraft F, som trekker loddet mot likevektsstillingen, og en kraft S, som trekker loddet i pendelsnoren. Når loddet passerer likevektsstillingen loddrett under opphengningspunktet, er kraften F lik null, men loddet har fart og fortsetter mot motsatt side. Loddet blir nå påvirket av en kraft som er rettet mot bevegelsen, og som vokser med utslaget. Til slutt stopper loddet og begynner å bevege seg innover mot likevektsstillingen igjen. Pendelens svingetid er uavhengig av pendelens masse (tyngde) og av utslagenes størrelse, såfremt de er små. Svingningene er isokrone.
Tyngdependel
Et legeme som kan svinge regelmessig omkring en likevektsstilling på grunn av tyngdens påvirkning, kalles en tyngdependel. Den svinger om en fast akse som ligger høyere enn legemets tyngdepunkt.
En idealisert pendel, hvor man tenker seg at all masse er samlet i ett punkt, som er opphengt i en vektløs tråd, kalles en matematisk pendel. En god tilnærmelse til dette er en liten blykule som henger i en tynn, lett tråd.
Pendelens lengde er avstanden fra aksen, opphengningspunktet, til tyngdepunktet. Når pendelen er i ro, er tyngdepunktet loddrett under aksen. Når pendelen svinger, beveger tyngdepunktet seg i en sirkelbue. Svingningens største utslag til en av sidene kalles amplituden. For utslag mindre enn 5° gjelder med god tilnærmelse for den matematiske pendelen, og også for den enkle blykulependelen, at svingetiden T er gitt av formelen
\[T= 2\pi \sqrt{\frac{l}{g}} \]
der l er pendelens lengde og g er tyngdens akselerasjon.
Svingetiden er uavhengig av amplituden (isokrone svingninger) og av pendelens masse. Formelen viser at pendelen kan brukes som tidsmåler og for bestemmelse av tyngdens akselerasjon.
Svingetiden regnes for en hel svingning, for eksempel fra pendelen er i en ytterstilling og til den er tilbake i samme ytterstilling.
Andre typer
Ballistisk pendel
En ballistisk pendel er en pendel som brukes til å måle hastigheten til prosjektiler. Når et prosjektil blir skutt inn i for eksempel en trekloss eller en sandsekk som henger i en snor, kan man av pendelens utslag beregne prosjektilets fart.
Elastisk pendel
Et legeme som kan svinge regelmessig omkring en likevektsstilling på grunn av elastiske krefter, kalles en elastisk pendel. En enkel form for en slik pendel er et lodd som henger i en skruefjær av stål. Svingetiden for en slik pendel er
\[T=2\pi \sqrt{\frac{m}{k}}\]
hvor m er massen av loddet, og k er stivheten i fjæren. Denne formelen gjelder også for store svingeutslag.
Svingetiden for en elastisk pendel er uavhengig av tyngdekraften.
Torsjonspendel
Et legeme som henger i en metalltråd, kan utføre dreiesvingninger. Det kalles en torsjonspendel.



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.