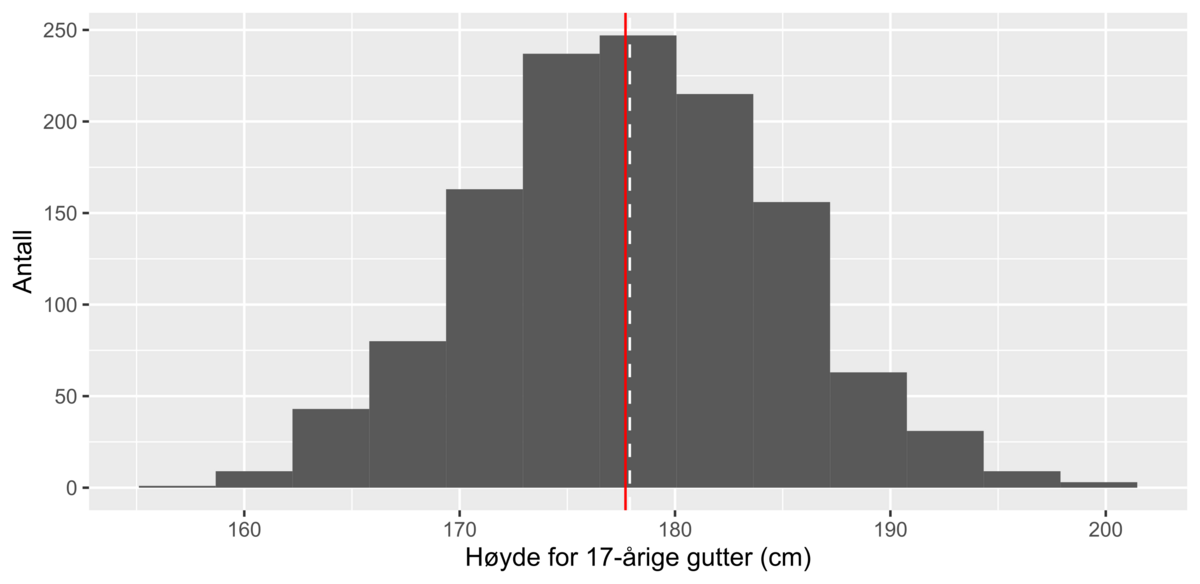
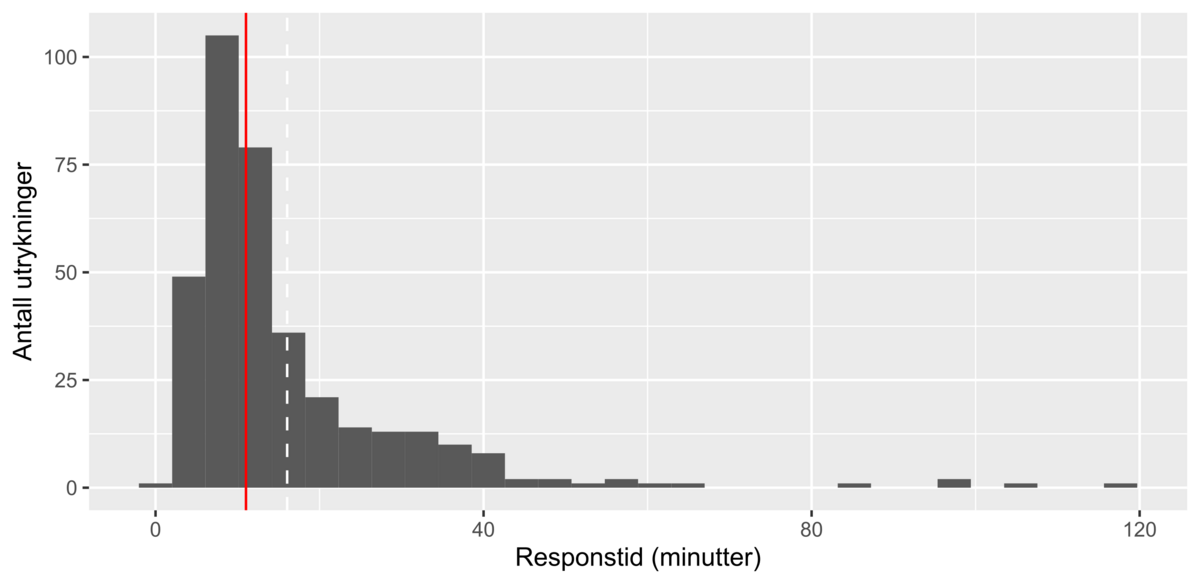
Median er i statistikk et tall som brukes til å oppsummere hva som er en vanlig verdi i en samling av tall. Når tallene sorteres i stigende rekkefølge, er medianen det midterste tallet. Hvis antall tall er et partall, er medianen gjennomsnittet av de to midterste tallene.
Medianverdien deler tallmaterialet i to: Den ene halvparten av tallene har lavere verdi enn medianen, og den andre halvparten av tallene har høyere verdi enn medianen.
Medianen er det samme som andre kvartil eller 50-prosentilen i tallmaterialet.




Kommentarer (2)
skrev Kim Ulriksen
svarte Jan Bjørnstad
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.