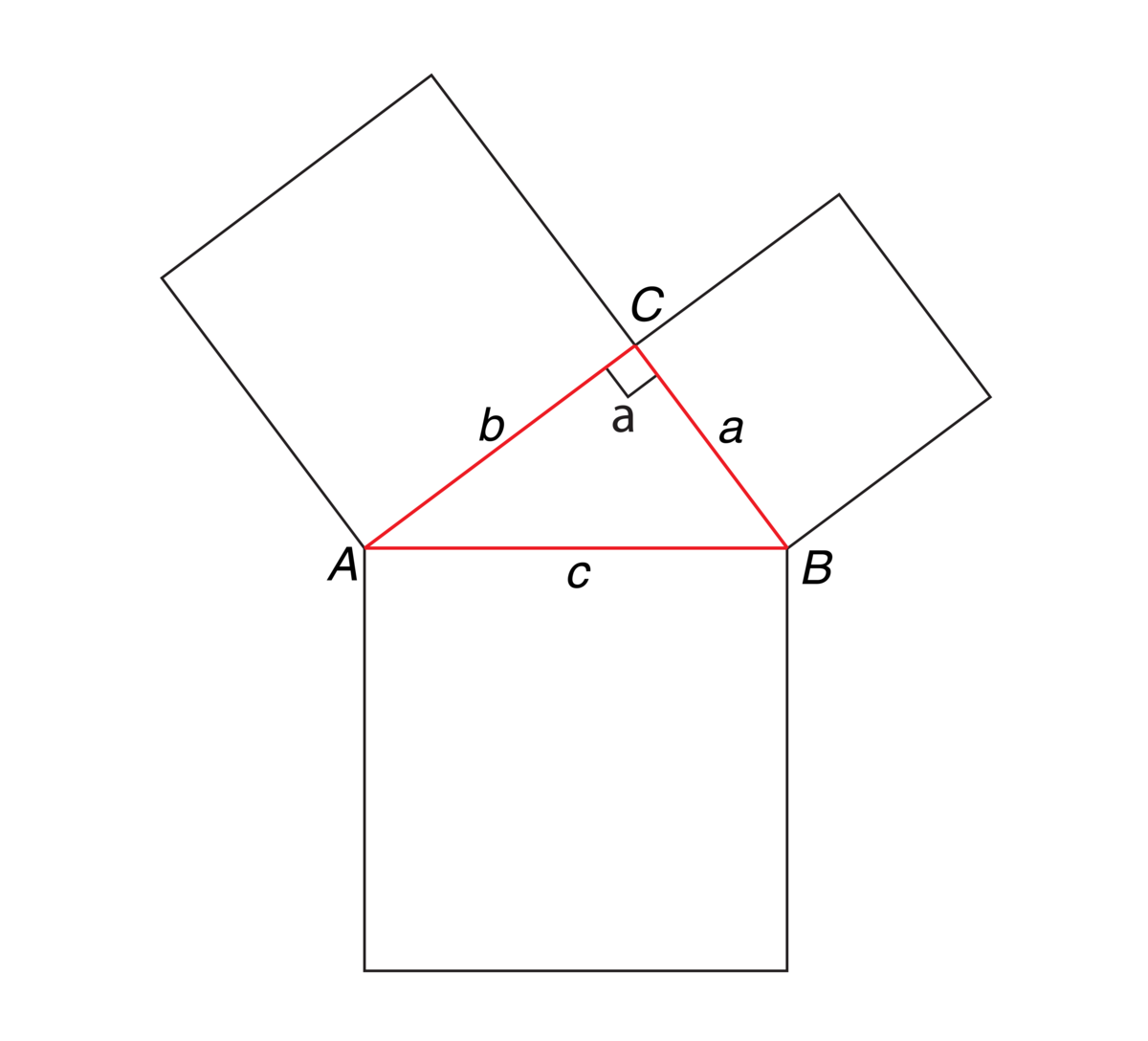
Pytagoras' setning er en læresetning i geometrien som beskriver forholdet mellom sidene i en rettvinklet trekant. Setningen sier at kvadratet på hypotenusen i en rettvinklet trekant er lik summen av kvadratene på de to katetene. Hvis katetenes lengder er a og b og hypotenusen har lengde c, er altså a2 + b2 = c2.
Faktaboks
- Også kjent som
-
Pytagoras' læresetning, Pytagoras' sats, den pytagoreiske læresetning
Det finnes uendelig mange hele tall som oppfyller denne betingelsen. Ett eksempel er de tre tallene a = 3, b = 4, c = 5. Slike tall kalles av og til pytagoreiske tall, og de har spilt en viss rolle i numerologiske spekulasjoner (tallmystikk).
Setningen har navn etter Pytagoras, men det er vist at både denne setningen og metoden til å bestemme pytagoreiske tall var kjent allerede av babylonerne cirka 2000 fvt. Det er imidlertid mulig at Pytagoras var den første til å bevise setningen.
For trekanter som ikke er rettvinklede, det vil si at vinkelen α = ∠ACB ikke er 90°, gjelder den utvidede pytagoreiske læresetningen, ofte kalt cosinussetningen: c2 = a2 + b2 – 2ab · cos α.



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.