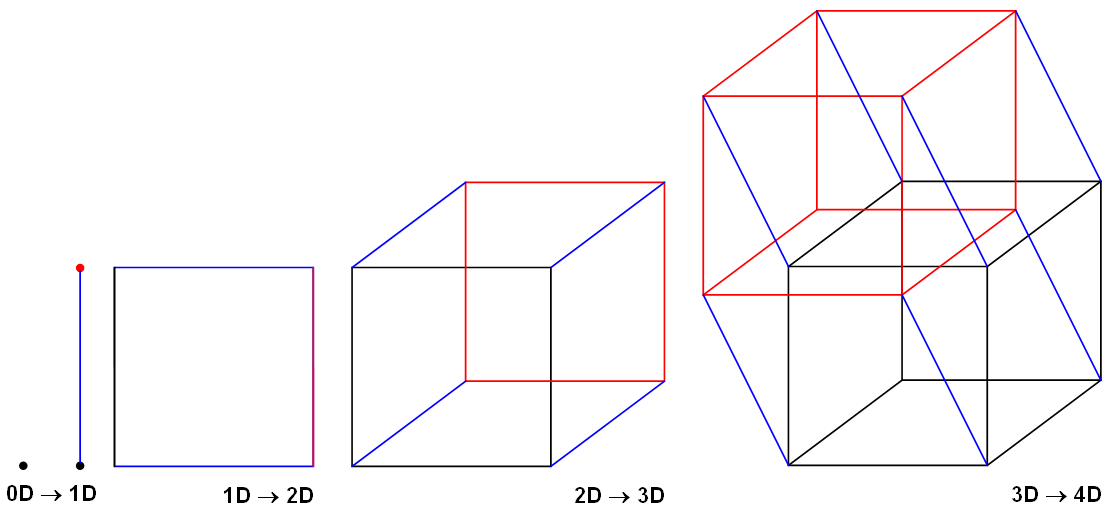
En hyperkube er en generalisering av den vanlige tredimensjonale kuben og det todimensjonale kvadratet til \(n\) dimensjoner. Mens et kvadrat har fire hjørner og en kube åtte hjørner, vil den firedimensjonale hyperkuben ha 16 hjørner, den femdimensjonale 32 hjørner og den generelle \(n-\)dimensjonale \(2^n\) hjørner.
På samme måte som kuben kan konstrueres ved å ta to like kvadrater, for eksempel som topp og bunn, og forbinde korresponderende hjørner i de to kvadratene, kan den \(n-\)dimensjonale hyperkuben anses for å bestå av to hyperkuber av dimensjon \(n-1\), der korresponderende hjørner er forbundet med kanter vinkelrett på toppen og bunnen. Alle sidekantene som forbinder to hjørner, både de som er i bunnen eller toppen, og de nye som forbinder toppen og bunnen, har samme lengde.



Kommentarer (2)
skrev Tor-Ivar Krogsæter
Jeg er usikker på om illustrasjonen av 4D-kuben egentlig reflekterer den fjerde dimensjonen tilstrekkelig godt. I hver overgang fra n dimensjoner til n+1 dimensjon, kopieres representasjonen i n dimensjoner til alle mulighetene i n+1 dimensjoner. Kvadratets fire kanter AB, BC, CD, CA forlenges alle i den nye z-aksen. Denne samme forøkningen er ikke synliggjort på noen god måte fra 3D- til 4D-figuren. Nå er det vanskelig å representere fire dimensjoner, og i alle fall når en prøver å gjøre det som en tredimensjonal figur projisert på et todimensjonalt medium, men det er da likevel mange flotte representasjoner (som t.d. 3D-skrevede figurer) som langt bedre demonstrerer hva som skjer i overgangen fra tre til fire dimensjoner. Personlig anbefaler jeg denne Numberphile-videoen med prof. Carlo Heinrich Séquin: https://www.youtube.com/watch?v=2s4TqVAbfz4.
svarte Tor-Ivar Krogsæter
Matt Parker har dessuten ei forelesning på nett som viser andre måter å illustrere hvordan en kan forestille seg en 4D-kube i 3D, her fra der han snakker om hvordan skyggen av først en 3D-kube ser ut for folk i en 2D-verden, deretter hvordan skyggen av en 4D-kube ser ut i en 3D-verden: https://youtu.be/1wAaI_6b9JE?t=2757
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.