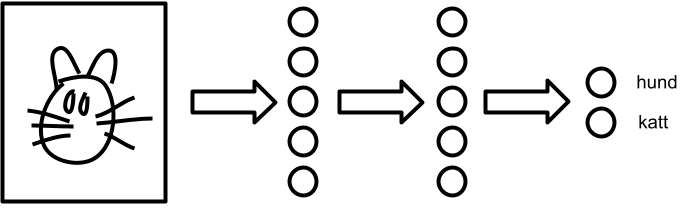
Nevrale nettverk er en teknikk som brukes som byggesteiner innen maskinlæring og kunstig intelligens. De kan ses på som en veldig grov forenkling av hvordan nervecellene i hjernen fungerer. De underliggende prinsippene er svært enkle: nevrale nettverk er bygd opp av «nevroner» (prosesseringsenheter) og koblinger mellom disse nevronene.
kunstig nevralt nettverk
Nevronene påvirker hverandre på forskjellig måte. Hvordan nevronene påvirker hverandre, bestemmes når nettverket lærer. Dette er basert på enkle matematiske prinsipper. Rent teknisk er dette matrisemultiplikasjon, ikke-lineære funksjoner (som for eksempel hyperbolsk tangens) og derivasjon.
Styrken til nevrale nettverk er at de kan lære sammenhenger mellom inngangs- og utgangs-data, for eksempel bilder (som teknisk sett er en matrise med piksler) og hva vi ser i et bilde (en kategori).
Se for deg bilder av katter og hunder; det er ikke lett å matematisk formulere hvordan en katt eller en hund ser ut. Men gitt at man har mange bilder av katter og hunder, kan det nevrale nettverket selv finne ut hvordan forskjellen skal representeres internt i det nevrale nettverket.
Man kan si at det nevrale nettverket bestemmer selv sin egen matematiske funksjon for å beskrive katter og hunder. Det er dette som er grunnlaget for dyplæring.
Det nevrale nettverket "ser" på bildet av en katt, og sender signaler gjennom nettverket. I det siste laget "forteller" nettverket om det ser en katt eller en hund.
Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.