Kubikktall er tallene man får ved å opphøye de naturlige tallene i 3. potens. For eksempel er kubikktallet av tallet 4 lik 64 fordi \(4^3 = 64\).
Faktaboks
- Uttale
- kubˈikktall
- Etymologi
- av kubikk-
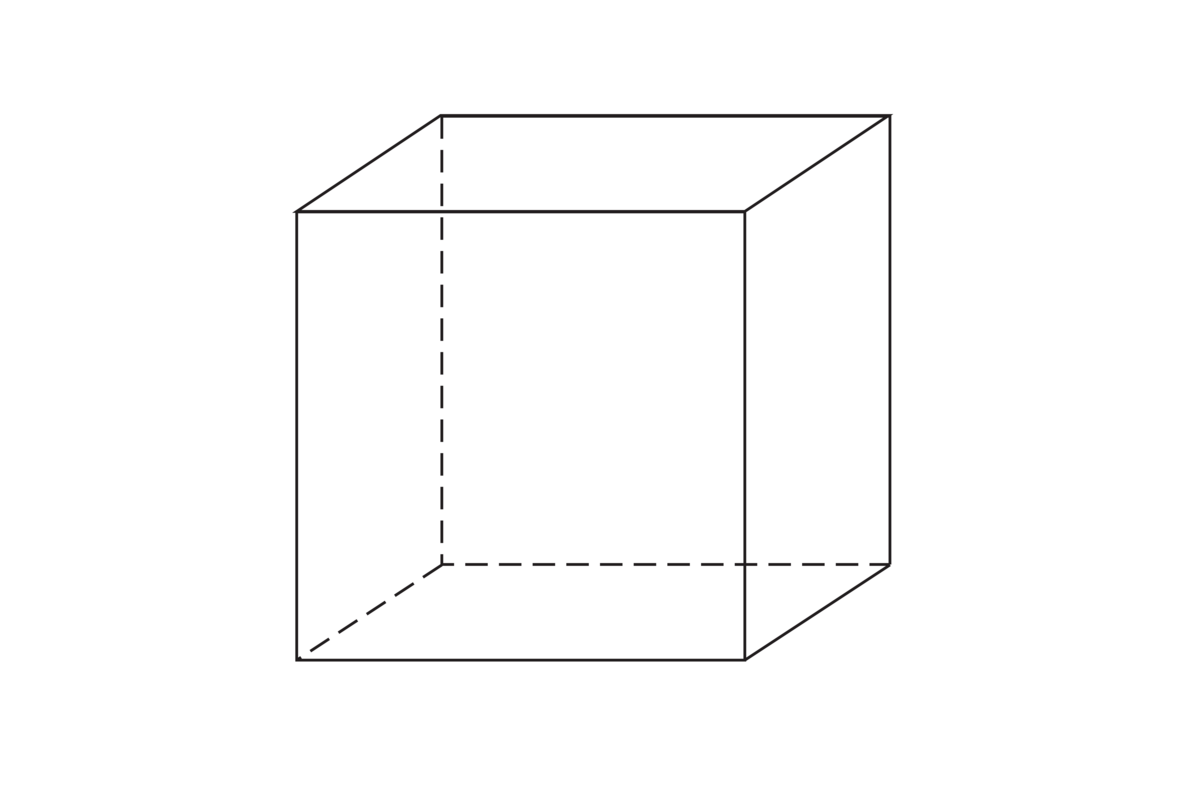
Hvert kubikktall n3 tilsvarer volumet av en kube der sideflatene har lengde lik n.
Kubikkroten (tredjeroten) av et kubikktall er lik det tallet som ble opphøyd i 3. potens. For eksempel er kubikkroten av tallet 64 lik 4, fordi 43 = 64.
Summen av de n første kubikktallene er lik 2. potens av summen av de n første naturlige tallene. Det vil si 13 + 23 + 33 + ... + n3 = (1 + 2 + 3 + ... + n)2 eller
\[\sum_{x=1}^n x^3 = \left(\frac{n(n+1)}{2}\right)^2\]
Dette er et resultat som allerede oldtidens grekere kjente til.



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.