Hypergeometrisk fordeling er den statistiske sannsynlighetsfordelingen til antall individer med en bestemt egenskap i et tilfeldig utvalg fra en populasjon (jamfør utvalgsundersøkelse).
Alle individene i populasjonen har samme sannsynlighet for å komme med i utvalget. Hvis M av totalt N individer i populasjonen har egenskapen, og det trekkes et utvalg på n enheter, så er sannsynligheten for at vi får x enheter med kjennetegnet i utvalget lik \[\frac{\binom{M}{x}\binom{N-M}{n-x}}{\binom{N}{n}}\] hvor parentesuttrykkene ovenfor på formen \(\binom{a}{b}\) vil si binomialkoeffisienten \(\frac{a(a-1) \dotsc (a-b+1)}{1 \cdot 2 \cdot 3 \cdot \dotsc \cdot b}\), se binomisk fordeling. Når N er stor i forhold til n er denne sannsynligheten tilnærmet lik sannsynligheten for verdien x i en binomisk fordeling med p = M/N.
Eksempel: Antallet arbeidsledige i ett enkelt tilfeldig utvalg på 30 personer fra en befolkning på 100, hvorav 10 er arbeidsledige, er hypergeometrisk fordelt med N=100, M=10 og n=30. Ved å bruke formelen ovenfor, finner vi at sannsynligheten for at det er 3 arbeidsledige i utvalget blir 0,28, mens sannsynligheten for at det ikke er noen arbeidsledige i utvalget er lik 0,02.


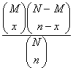



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.