motsigelseskvadratet

Motsigelseskvadratet er et skjema innen den tradisjonelle logikken som uttrykker logiske forhold mellom bestemte typer setninger. Denne logikken, som er basert på subjekt-predikat-analyse av utsagn, ser det slik at kategoriske utsagn, det vil si utsagn som består av et subjekt, kopula (er) og et predikat, varierer langs to dimensjoner: De kan være enten universelle eller partikulære, og de kan være enten bekreftende eller benektende. Dette gir fire former for kategoriske utsagn som tradisjonelt betegnes med bokstavene A, E, I og O:

A: «Alle S er P» (universelt bekreftende)

E: «Ingen S er P» (universelt nektende)

I: «Noen S er P» (partikulært bekreftende)

O: «Noen S er ikke P» (partikulært nektende)

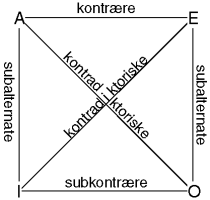
De logiske forhold mellom disse fire typene utsagn settes opp i motsigelseskvadratet:

At to utsagn A og B er kontradiktoriske, vil si at dersom A er sann, er B falsk, eller motsatt. At to utsagn er subkontrære vi si at ikke begge kan være falske, men begge kan være sanne. At et utsagn B er subalternate til et utsagn A vi si at dersom A er sant, så er B sant.

I henhold til den klassiske logikken så er I subordinate til A og O subordinate til E. Moderne logikk som er basert på en argument-funksjonsstruktur, benekter den siste antagelsen. Der representeres A som (∀x) (Fx ⊃Gx) (leses som «for alle objekter x gjelder det at hvis x har egenskapen F, så har x egenskapen G»), mens I representeres som (∃x) (Fx&Gx) (leses som «det finnes i det minste et objekt som både er F og G»). Det første utsagnet er hypotetisk og forutsetter derfor ikke at det finnes noe objekt med egenskapen F, mens det gjør det andre. Derfor kan et utsagn på formen A være sant, og et utsagn på formen I være usant. Et lignende resonnement kan gjøres for forholdet mellom E og O.