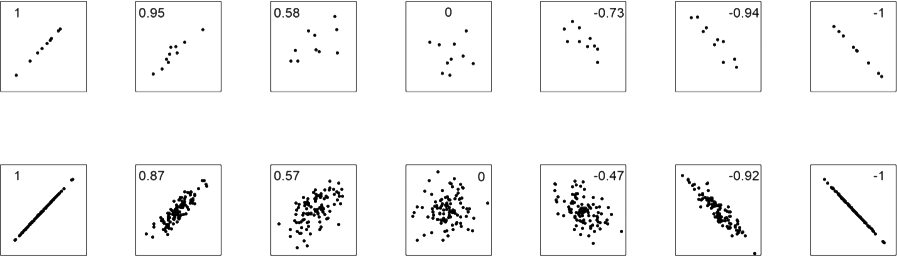
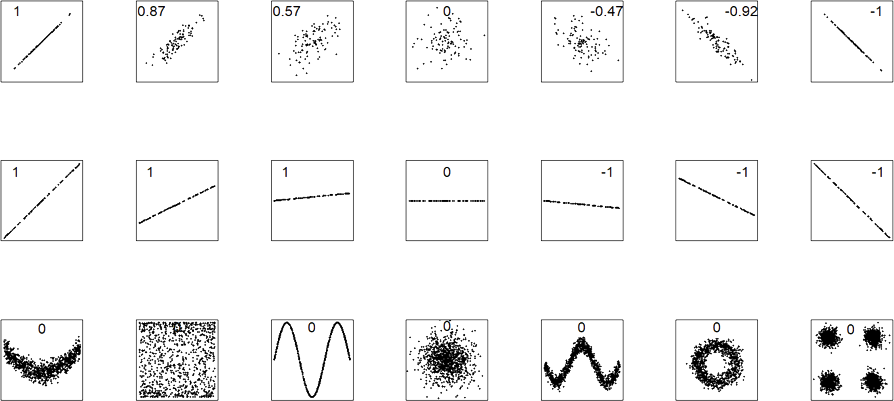
Korrelasjon er et statistisk mål på hvor mye to målbare størrelser henger sammen med hverandre. For eksempel betyr en positiv korrelasjon mellom høyde og vekt at høye folk ofte er tyngre enn lave folk.
Korrelasjon kalles også samvariasjon. I dagligtale kan man ofte bruke sammenheng eller statistisk sammenheng.
Korrelasjon mellom to størrelser trenger ikke å bety at den ene størrelsen er årsak til den andre.
Positiv korrelasjon betyr at høye verdier av den ene størrelsen ofte vil finnes sammen med høye verdier av den andre størrelsen. Noen eksempler på størrelser som har positiv korrelasjon er røyking og lungekreftrisiko, matinntak og fedme, lungevolum og oksygenopptak, og antall studietimer og karakterene man får.
Negativ korrelasjon er det når høye verdier av den ene størrelsen generelt finnes sammen med lave verdier av den andre. Det er for eksempel negativ korrelasjon mellom verdien på en bil og hvor gammel bilen er. Eldre biler er generelt billigere enn nye biler.
Styrken av korrelasjonen gis ved korrelasjonskoeffisienten. En korrelasjonskoeffisient er et tall mellom −1 og 1 som oppsummerer graden av samsvar. Et positivt tall betyr at det er positiv korrelasjon, og et negativt tall betyr at det er negativ korrelasjon. For eksempel fant man i en undersøkelse en korrelasjon på 0,37 mellom høyde og vekt for 7000 voksne kvinner.
Jo nærmere 1 eller −1 tallet er, jo sterkere er sammenhengen mellom de to størrelsene. I en gruppe med 67 voksne kvinner og menn var det for eksempel en korrelasjon på 0,94 mellom den høyden man ble målt til å ha og den høyden man trodde man hadde.
Korrelasjonskoeffisienter påvirkes ikke av måleenheten. Det betyr at du får samme tall for korrelasjonen hvis du måler høyde og vekt i meter og kilo, som du får hvis du måler det i centimeter og gram.
Flere eksempler på korrelasjonskoeffisienter. Den øverste rekken viser hvordan korrelasjonskoeffisienten varierer i ulike situasjoner der punktene ligger mer eller mindre langs en rett linje. Den midterste rekken viser at når punktene ligger på en stigende rett linje, så er korrelasjonskoeffisienten alltid 1, og når punktene ligger på en synkende rett linje, er korrelasjonskoeffisienten alltid -1. Midt-kolonnen i figuren viser eksempler på at når det ikke er noen sammenheng mellom de to størrelsene, så er korrelasjonskoeffisienten 0. Den nederste rekken viser at selv om korrelasjonskoeffisienten er 0, kan det være klare (men ikke-lineære) sammenhenger mellom de to størrelsene.
Dersom de to målbare størrelsene er uavhengige, er korrelasjonskoeffisienten 0 eller nær 0. For eksempel vil det være uavhengighet og null korrelasjon mellom høydemålinger som gjøres på en helsestasjon og temperaturen utendørs den dagen målingene blir gjort. Uavhengighet betyr i denne sammenhengen at kunnskap om den ene størrelsen ikke forteller oss noe om verdiene til den andre størrelsen: Utetemperaturen gir oss ingen hint om hva høydemålingene vil være, og høydemålingene kan ikke brukes til å si noe om temperaturen utenfor huset.
En korrelasjonskoeffisient på 0 betyr imidlertid ikke nødvendigvis at de to størrelsene er uavhengige. Hvis det er en annen sammenheng mellom de to målbare størrelsene enn en rett linje, kan korrelasjonskoeffisienten allikevel bli 0. For å unngå å trekke feil konklusjon, må man derfor alltid tegne opp målingene i et diagram.
Korrelasjon mellom størrelser betyr ikke nødvendigvis at det er en årsakssammenheng (også kalt en kausal sammenheng) mellom dem.
Anta for eksempel at man i en befolkning finner en positiv korrelasjon mellom bruk av lesebriller og det å ha hjerte- og karsykdommer. Da kan man ikke uten videre konkludere med at brillene øker risikoen for hjertesykdommer, eller at hjertesykdom fører til at folk trenger briller. En annen forklaring på den positive korrelasjonen kan være at både brillebruk og hjertesykdommer skyldes økende alder, og at brillebruk og hjertesykdommer derfor ofte forekommer sammen. I dette tilfellet skyldes altså korrelasjonen at begge egenskapene har kausal sammenheng med en tredje egenskap, nemlig høy alder.
Store norske leksikon
Kommentarer
Kommentaren din publiseres her. Fagansvarlig eller redaktør svarer når de kan.
Du må være logget inn for å kommentere.