Avstandsloven og første cosinuslov er beregningsmåter for å finne belysningsstyrken i et punkt med utgangspunkt i lysstyrken fra en punktformet lyskilde.
Faktaboks
- Også kjent som
-
Lysberegning etter punktmetoden
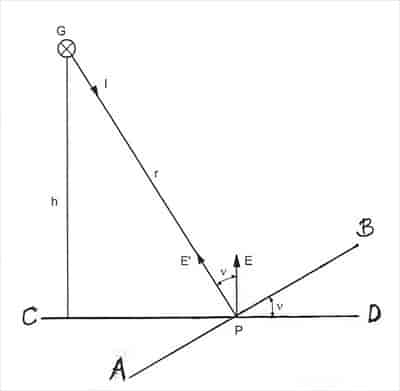
Avstandsloven gjelder dersom en ønsker å finne belysningsstyrken (E) i et punkt (P) som ligger på en flate som står vinkelrett på innfallende lys (A-B på fig.1).
Første cosinuslov gjelder dersom punktet ligger i et plan som står i en vinkel v i forhold til en flate vinkelrett på innfallende lys (C-D på fig.1).



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.