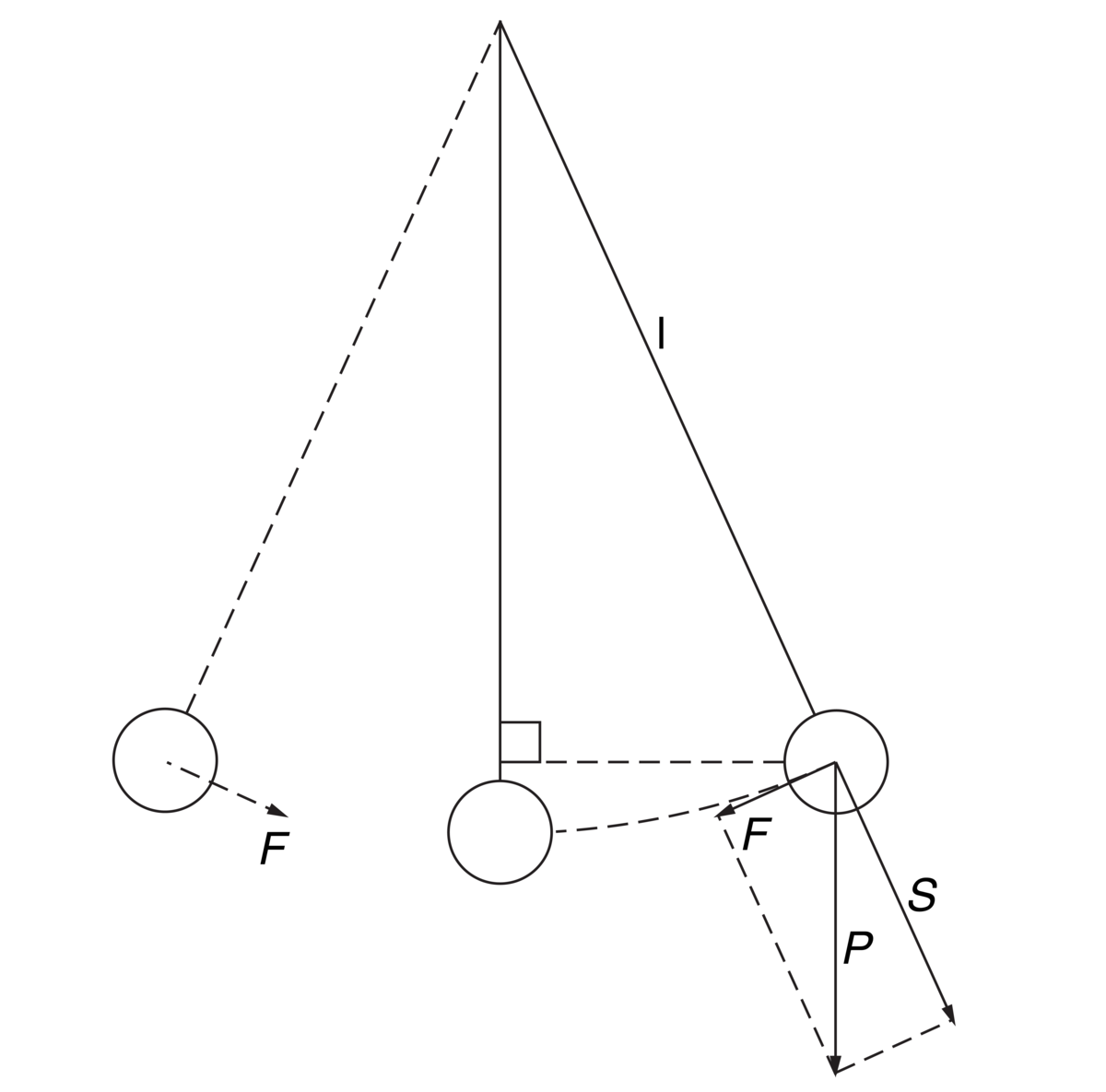
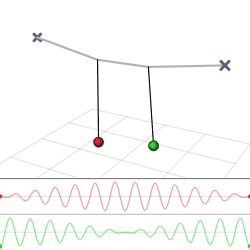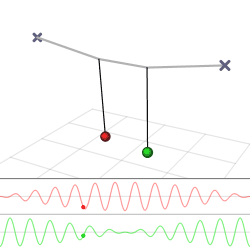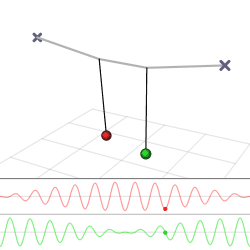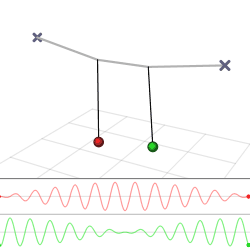
Figur 1 viser en svingende pendel. Den er eksempel på en mekanisk svingebevegelse. Andre typer systemer kan også anta en svingebevegelse, for eksempel i en elektrisk svingekrets der en kondensator og en spole er koplet i serie.
I figuren er det tyngdekraften som får pendelen til å henge loddrett med loddet i laveste stilling, likevektsstillingen. Blir loddet trukket ut til siden vil det bevege seg langs en sirkelbane og komme høyere i tyngdefeltet. Da får det stillingsenergi. Blir loddet sluppet, vil tyngdekraften trekke det tilbake. Da får loddet fart og går forbi likevektsstillingen med maksimal bevegelsesenergi til det stopper i en ytterstilling på motsatt side. Så beveger loddet seg mot likevektsstillingen igjen. Pendelen begynner å svinge.
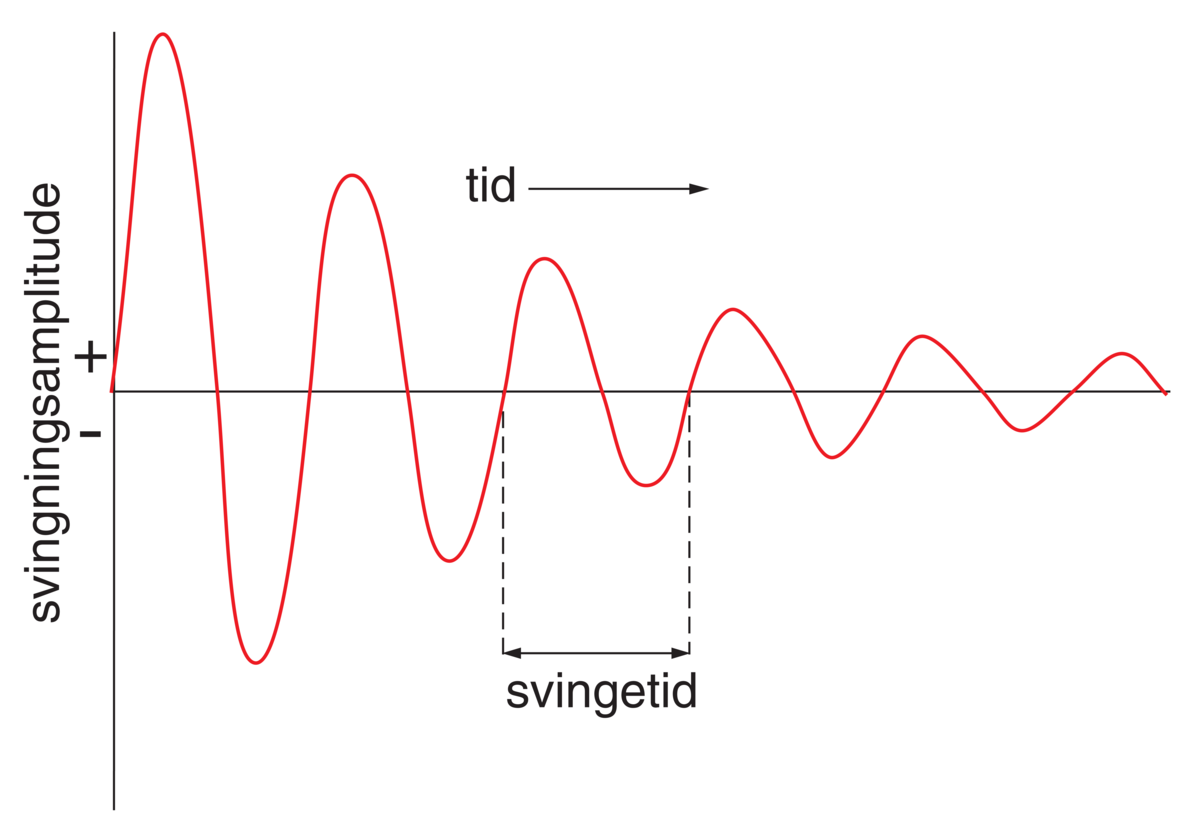
Det største utslaget til hver side kalles amplituden. Tiden som går med fra pendelen er i en ytterstilling og til den er tilbake i samme ytterstilling, kalles perioden. Antall perioder i et sekund kalles frekvens. En pendel har stillingsenergi i ytterstillingene og bevegelsesenergi i likevektsstillingen. Slik energiveksling opptrer i alle svingeformer.
Når et legeme som svinger er utsatt for en kraft mot likevektsposisjonen som er proporsjonal med avstanden fra likevektsposisjonen, kalles svingningen en harmonisk svingebevegelse. En slik bevegelse kan matematisk beskrives med en sinus- eller cosinusfunksjon.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.