potens – matematikk – Store norske leksikon

Potens er i matematikk et produkt av flere like faktorer, det vil si et tall eller uttrykk som er multiplisert med seg selv gjentatte ganger. n-te potens av tallet a skrives aⁿ og betyr a multiplisert med seg selv n ganger. Dette kalles «a opphøyd i n-te» eller bare «a i n-te».

Faktaboks

Uttale: potˈens
Etymologi: av latin

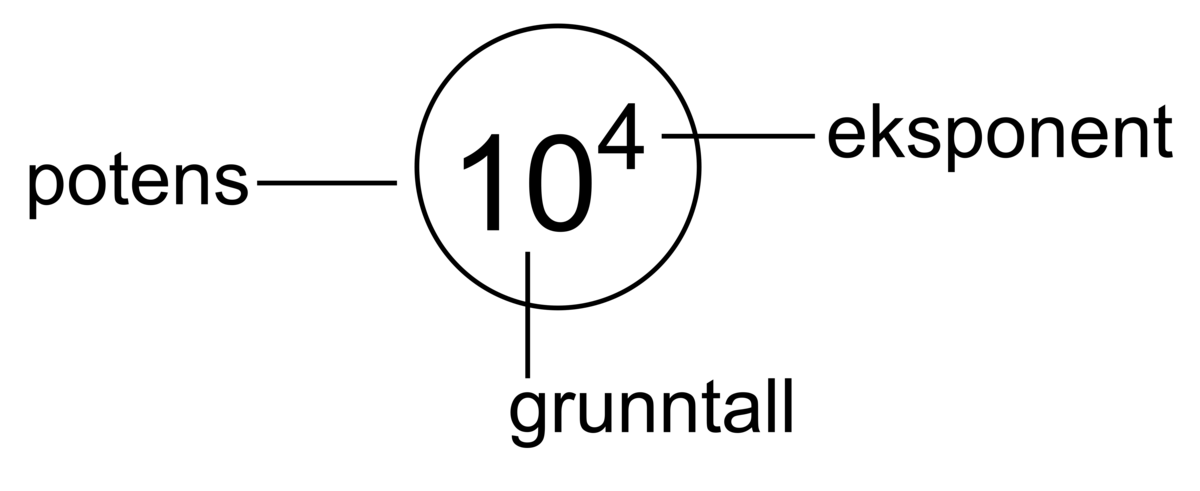
Tallet a er potensens grunntall, og n er eksponenten, som her er et naturlig tall (1, 2, 3, ...).

Eksempel: 2 opphøyd i 3 er 2³=2·2·2=8. Her er grunntallet 2 og eksponenten 3. Eksponenten angir hvor mange faktorer det er i produktet, og alle faktorene er lik grunntallet.

Hvis eksponenten er negativ, kan man bruke følgende regel: a⁻ⁿ=\(\frac{1}{a^n}\)

Eksempel: 2⁻³=\(\frac{1}{2^3}\)=\(\frac{1}{2·2·2}\)=\(\frac{1}{8}\)

Potenser blir for eksempel brukt for å angi areal og volum. Et kvadrat med sidelengde a har areal lik a². En kube med sidelengde a har volum lik a³.

Betegnelsesmåten for potens ble innført av René Descartes.

Regneregler

(aⁿ)^m=a^nm

Eksempel: (2³)²=(2·2·2)²=(2·2·2)·(2·2·2)=2·2·2·2·2·2=2⁶=2^3·2

a ⁿ ·a^m=a^n+m

Eksempel: 2³·2⁴=(2·2·2)·(2·2·2·2)=2·2·2·2·2·2·2=2⁷

Denne regelen gjelder fordi multiplikasjon av reelle tall oppfyller den assosiative loven.

\(\frac{a^n}{a^m}\)=a^n−m

Eksempel: \(\frac{2^5}{2^3}\)=\(\frac{2·2·2·2·2}{2·2·2}\)=2·2=2²=2⁵⁻³. Her ble brøken forkortet.

a⁻ⁿ=\(\frac{1}{a^n}\)

(a·b)ⁿ=aⁿ·bⁿ

Eksempel: (2·5)³=(2·5)·(2·5)·(2·5)=2·5·2·5·2·5=2·2·2·5·5·5=2³·5³

Denne regelen gjelder fordi multiplikasjon av reelle tall oppfyller den assosiative loven og den kommutative loven.

\(\left(\frac{a}{b}\right)^n\)=\(\frac{a^n}{b^n}\)

Eksempel:

\(\left(\frac{2}{5}\right)^3\)=\(\frac{2}{5}\)·\(\frac{2}{5}\)·\(\frac{2}{5}\)=\(\frac{2·2·2}{5·5·5}\)=\(\frac{2^3}{5^3}\)

Her ble regneregelen for multiplikasjon av brøk brukt.

Utvidelse av begrepet

Potensbegrepet kan utvides til vilkårlige rasjonale eksponenter ved at man definerer \(a^1 = a, \, a^0 = 1, \, a^{-p} = \frac{1}{a^p}, \, a^{\frac{p}{q}} = \sqrt[q]{a^p}\).

Ved hjelp av grenseoverganger defineres potensen for eksponenter som er reelle tall og ikke naturlige tall. For dette utvidede potensbegrepet gjelder samme regneregler som for heltallige eksponenter. Ved hjelp av identiteten xⁿ = e^nlnx kan man også generalisere potensbegrepet til eksponenter som er komplekse tall.

Funksjonen y = xⁿ kalles ofte potensfunksjonen.

Potens i geometrien

Begrepet potens brukes også i geometrien. Har man gitt et punkt P utenfor eller innenfor en sirkel og trekker en sekant til sirkelen gjennom P, vil produktet man får, når lengden langs sekanten fra P til første skjæringspunkt med sirkelen multipliseres med lengden fra P til det andre skjæringspunktet, være det samme for alle sekanter gjennom P. Dette produktet kalles punktets potens med hensyn til sirkelen.

Les mer i Store norske leksikon

Kommentarer

Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.

Du må være logget inn for å kommentere.

Fagansvarlig for Aritmetikk

Andrea Hofmann

Førsteamanuensis, Universitetet i Sørøst-Norge