En kurve som roterer om en akse, definerer en omdreiningsflate. Legemet som begrenses av denne flaten, kalles et omdreiningslegeme.
En torus er et omdreiningslegeme som fremkommer ved at en sirkel roterer om en akse som ikke skjærer sirkelen.
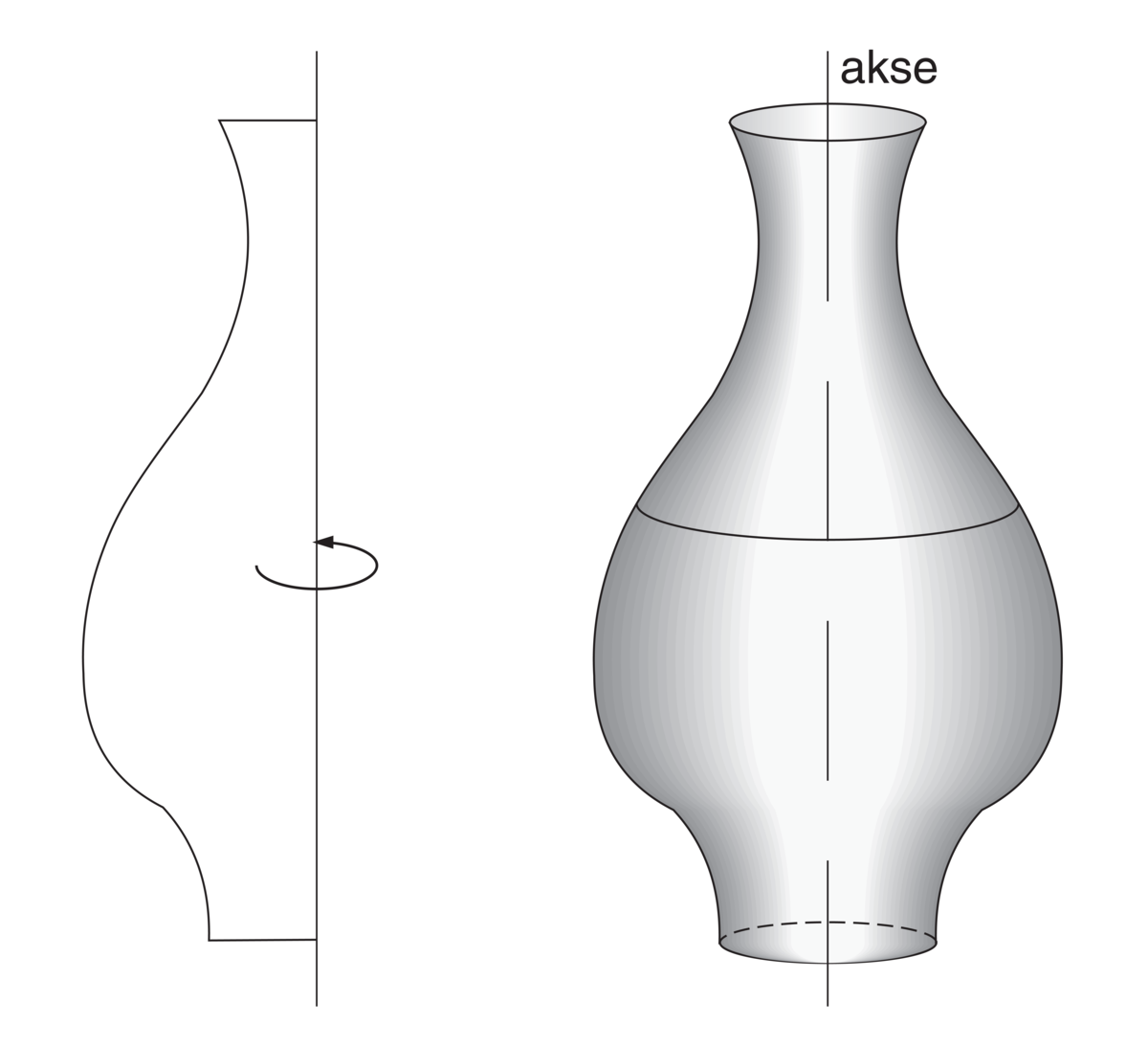
Omdreiningslegeme er i geometrien et legeme som fremkommer ved at en plan figur dreier seg om en akse som ligger i samme plan som figuren. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate.
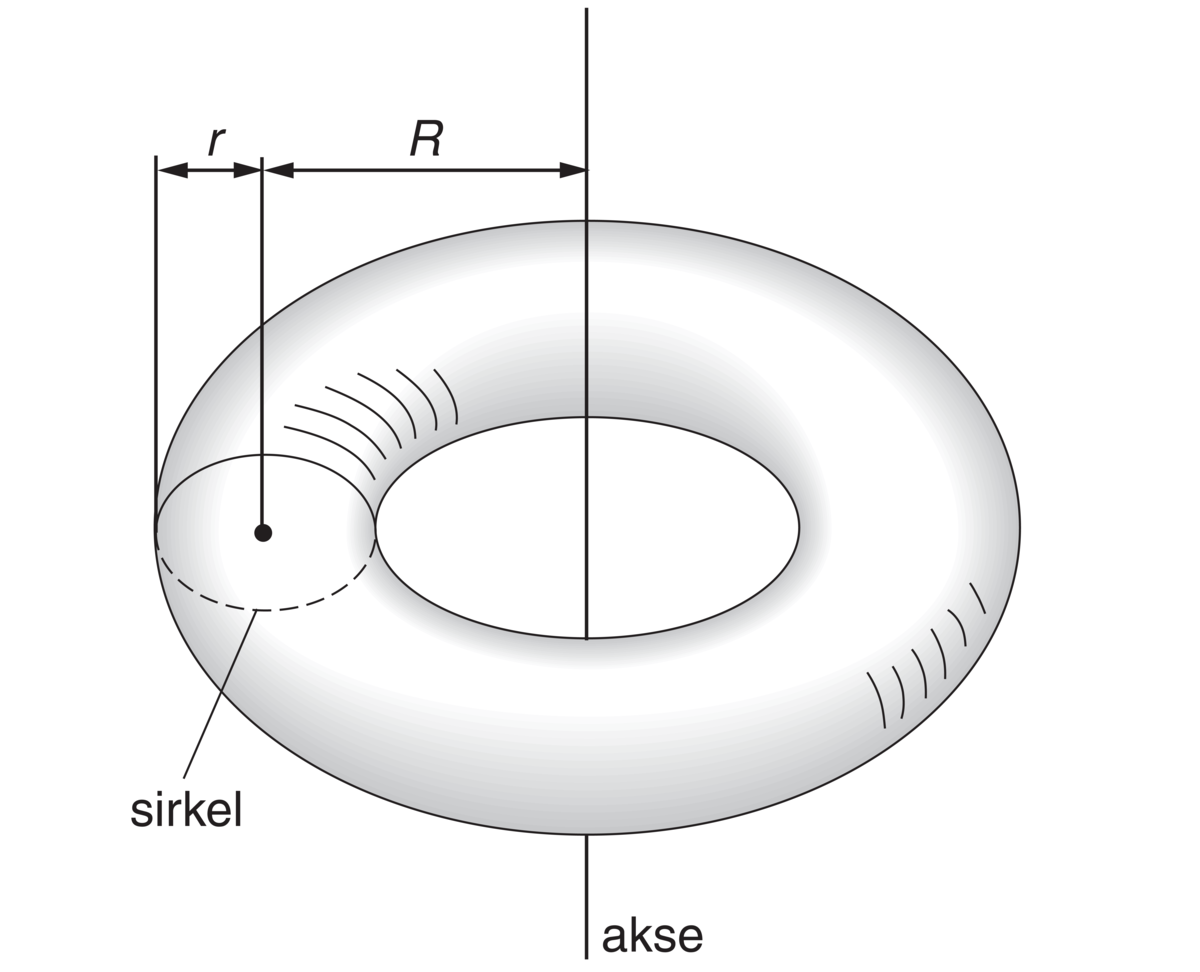
Noen eksempler på omdreiningslegemer er kule og ellipsoide, dessuten sylinder og kjegle (som begge oppstår ved rotasjon av en rett linje), omdreiningshyperboloide og paraboloide, dessuten torus (sirkelring), som fremkommer ved at en sirkel roteres om en akse som ikke skjærer sirkelen.
Guldins regler (også kalt de barysentriske reglene), som ble formulert av Paul Guldin, brukes til å bestemme arealet og volumet til omdreiningslegemer:
Disse reglene var i hovedsaken kjent av den aleksandrinske matematikeren Pappos (ca. 300 evt.), og de kalles derfor også ofte Pappos' regler.
Store norske leksikon
Kommentarer
Kommentaren din publiseres her. Fagansvarlig eller redaktør svarer når de kan.
Du må være logget inn for å kommentere.