høyeste grense, høydepunkt, største verdi, størst, størst mulig.
I matematikken er maksimum det største tall innenfor en gitt mengde reelle tall. Det minste blant dem kalles minimum. Selv begrensede tallmengder behøver ikke ha noe maksimum; for at et tall skal være maksimum i en mengde, må tallet tilhøre mengden. Det åpne intervallet <a, b> har dermed ikke noe maksimum, ettersom b ikke er med i intervallet, og det finnes ikke noe «største tall som er mindre enn b». I dette tilfellet sies b å være supremum for intervallet. Tilsvarende er a infimum for intervallet <a, b>. I et lukket intervall [a, b] er a minimum (og infimum) og b er maksimum (og supremum).
En reell funksjon som er kontinuerlig i et lukket og begrenset intervall [a, b] har alltid et maksimum og et minimum i intervallet, dvs. funksjonens verdimengde har et maksimum og et minimum. Med maksimum for en funksjon med reelle verdier forstås også undertiden det som mer presist kalles et lokalt maksimum, dvs. en funksjonsverdi som er større enn naboverdiene.
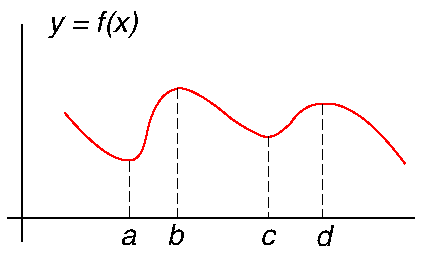
I figuren
har y = f(x) lokale maksima for x = b og x = d, lokale minima for x = a og x = c. Maksima og minima for funksjoner kalles med en samlebetegnelse for ekstremalpunkter. Når f er en deriverbar funksjon, kan punktene for lokale ekstremalpunkter bestemmes ved hjelp av differensialregning. I et ekstremalpunkt er den deriverte av funksjonen lik 0, det vil si at tangenten til funksjonen i punktet er vannrett (har stigningstall lik 0).