
konveks
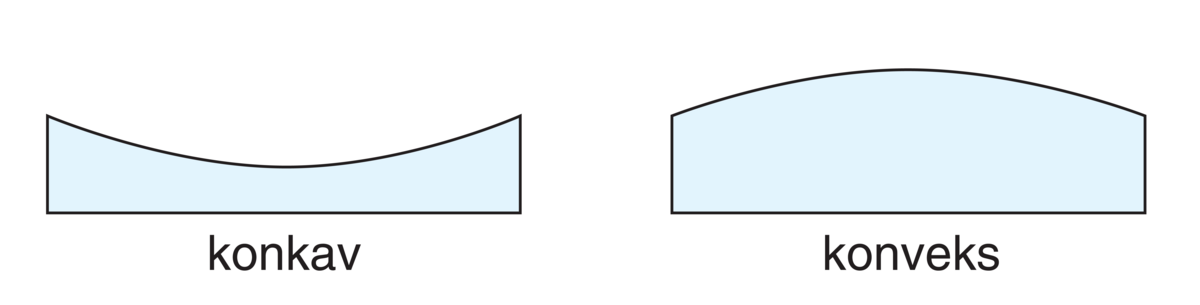
Konkav og konveks linse.
Geometri
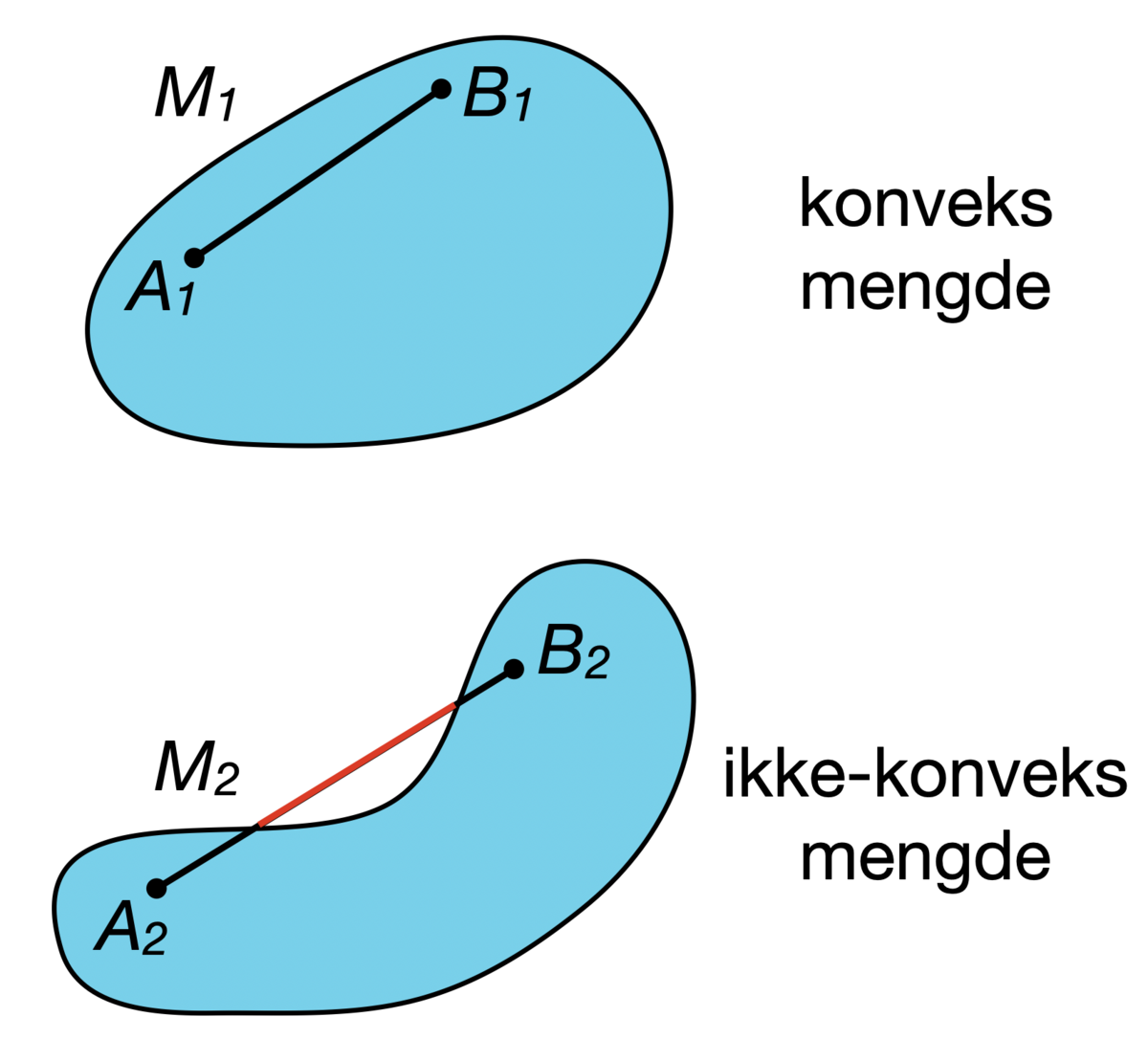
Mengden M1 er konveks fordi hele linjestykket mellom to punkter A1 og B1 alltid vil ligge innenfor M1. Mengden M2 er ikke-konveks fordi man kan finne to punkter A2 og B2 der et linjestykke mellom A2 og B2 vil inneholde punkter som ligger utenfor M2.
Det geometriske begrepet konveksitet dreier seg om hvordan linjestykker mellom punkter i mengden ligger i forhold til mengden.
En mengde M, som består av punkter i et plan eller i rommet, sies å være konveks hvis det følgende alltid gjelder: Hvis to punkter A og B hører til M, så hører også ethvert punkt på det rette linjestykket mellom A og B til M. En polygon eller et polyeder sies å være konveks hvis dets indre danner en konveks mengde. Figuren som viser en konveks linse illustrerer dette: mellom to vilkårlige punkter inne i linsen vil linjestykket mellom punktene også være inneholdt i linsen.
En kurve i planet sies å være konveks (også kalt konveks nedover eller konkav oppover) i et punkt hvis kurven i nærheten av punktet ligger over tangenten. Hvis kurven i nærheten av punktet ligger under tangenten, er kurven konkav (også kalt konveks oppover eller konkav nedover). Hele kurven sies å være konveks dersom det for alle par av punkter på kurven er slik at linjestykket mellom punktene ligger over kurven. Det innebærer at den delen av planet som ligger over kurven er en konveks mengde. Hvis kurven er grafen til en deriverbar funksjon er dette ekvivalent med at kurven er konveks i hvert enkelt punkt. Tilsvarende vil en kurve være konkav dersom linjestykket mellom to vilkårlige punkter ligger under kurven. Det innebærer at den delen av planet som ligger under kurven er en konveks mengde.
Hvis kurvens ligning er \(y = f(x)\) for en to ganger kontinuerlig deriverbar funksjon \(f\), vil kurven være konveks hvis \(f''(x)>0\), og konkav hvis \(f''(x)<0\), det vil si etter som den andrederiverte av funksjonen f er positiv eller negativ i nærheten av det punktet vi undersøker.
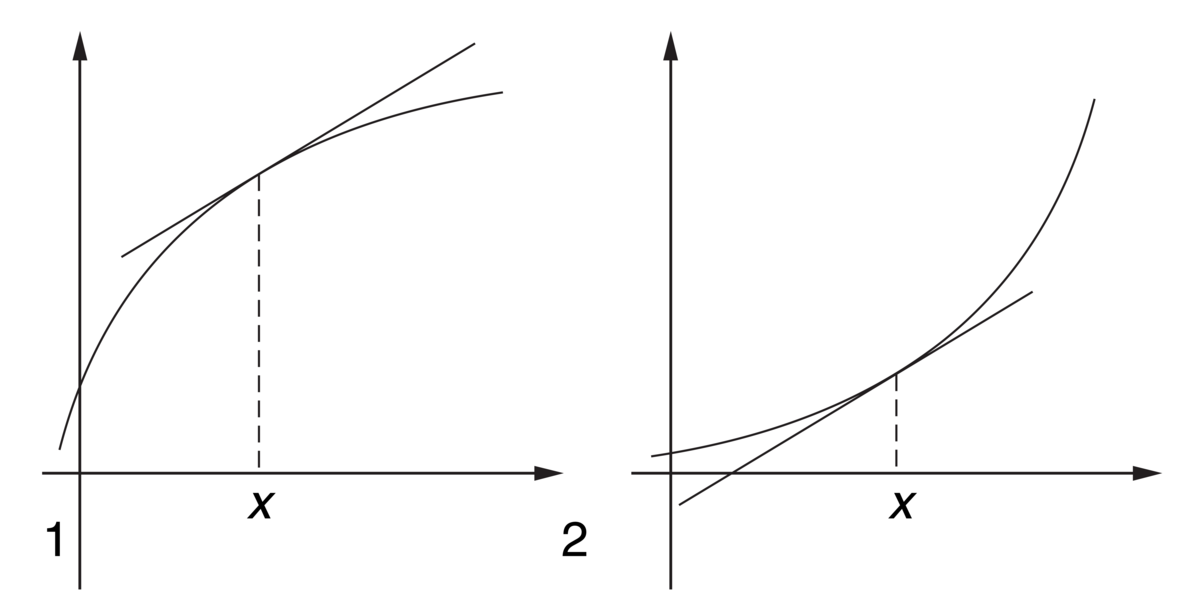
Konveksitet: 1) Konkav i punktet med abscisseverdi x. 2) Konveks i punktet med abscisseverdi x.



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.