I første halvdel av 1900-tallet ble kaosteori brukt innen ergotisk teori av flere, men til tross av dette ble ikke kaosteori definert og formalisert før i begynnelsen av siste halvdel av 1900-tallet. En av de første pionerene i dette henseende var Edward Lorenz som studerte enkle værfenomener på sin enkle datamaskin.
I 1960 var kapasiteten til datamaskinene alt for liten til å implementere realistiske simuleringer av atmosfæren, men det pågikk en del forsøk. Det var da Lorenz, nærmest ved et uhell, gjorde sin store oppdagelse. Han skulle gjenta en simulering og hadde en utskrift med tall med 3 desimaler fra datamaskinen (for eksempel 12,854). Da han startet en ny simulering med disse tallene, fikk han en helt annen predikert værutvikling. Årsaken var at minnet i datamaskinen avrundet med 6 desimaler (12,854123), altså mer nøyaktig enn utskriften. Den enkle konklusjonen var altså at tilsynelatende ubetydelige forskjeller i initialbetingelsene førte til svært forskjellige resultater etter noe tid.
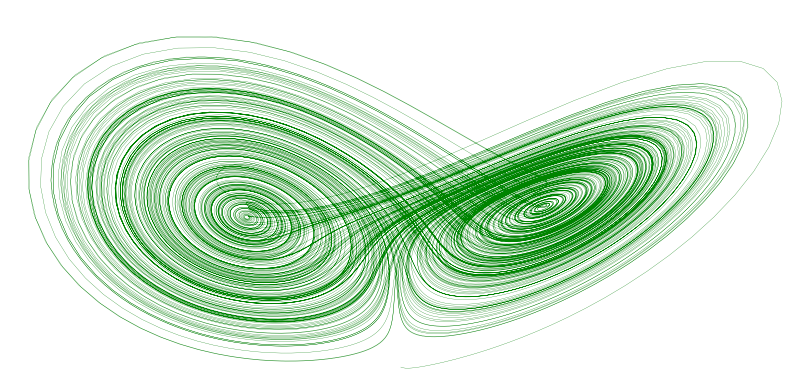
Hypotesen var at modellen ville komme i likevekt etter en stund (grafen ville stoppe i et punkt), eventuelt at den grafiske løsningen ville repetere seg selv etter en stund. Ingen av delene skjedde. Uforutsigbarheten fortsatte i det uendelige, men innenfor grensene av «sommerfuglvingene» (Lorenz-attraktorer, se figur). Med andre ord var det et slags system i kaoset.
Dette er den såkalte sommerfugleffekten, som la mye av grunnlaget for det man kaller deterministisk kaos.
I praktisk værvarsling har man forsøkt å løse noe av problemet med å sette i gang datamaskinene med tilnærmet samme startverdier mange ganger, såkalte ensembleprognoser.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.