Hyperbel er en geometrisk kurve som er et av kjeglesnittene. Den består av to adskilte deler.
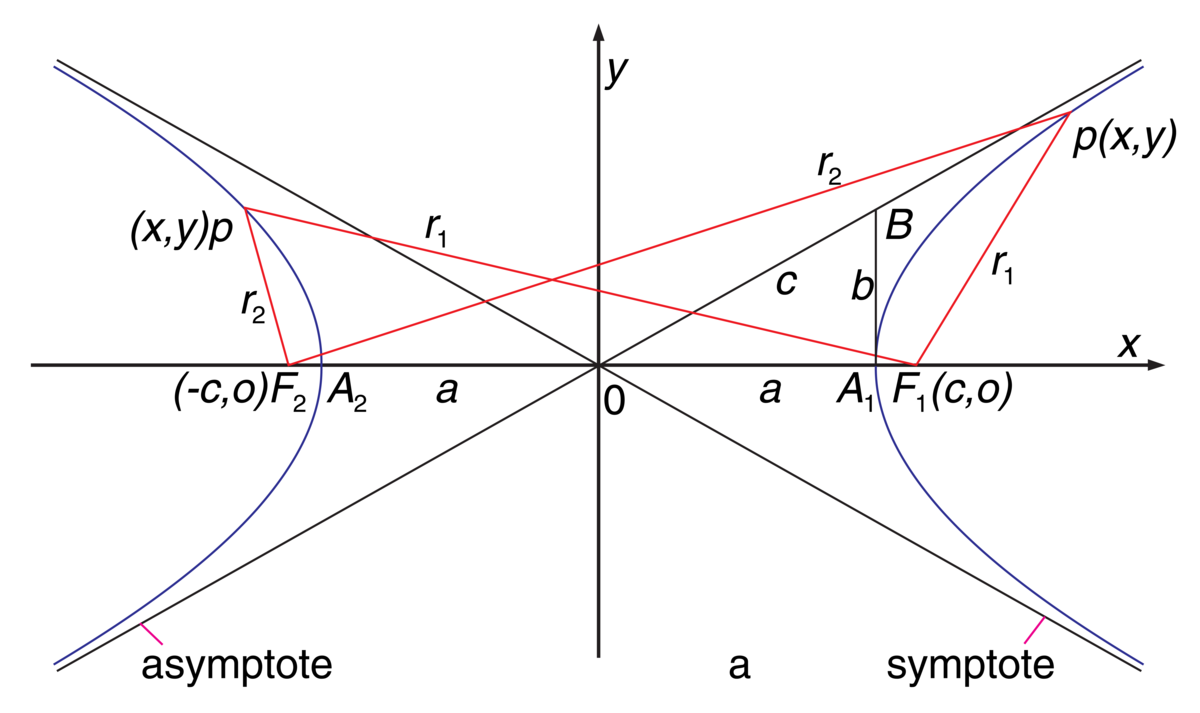
Matematisk kan en hyperbel beskrives som en plan kurve med den egenskapen at differensen mellom avstandene fra ethvert punkt P på kurven til to faste punkter F1 og F2, som kalles brennpunktene, er konstant (se figur). Denne konstante lengden kaller vi her 2a. Til høyre i figuren er r2−r1 = 2a, og til venstre er r1−r2 = 2a.
Hyperbelen har to symmetriakser. Den ene går gjennom brennpunktene og skjærer hyperbelen i to punkter A2 og A1, som vi kaller toppunktene. Den andre aksen står vinkelrett på den første midt mellom toppunktene, i hyperbelens sentrum O.
Dersom avstanden mellom brennpunktene settes lik 2c, kan ligningen for en hyperbel i et rettvinklet koordinatsystem, hvor x-aksen går gjennom brennpunktene og y-aksen gjennom hyperbelens sentrum O, skrives som
\[\frac{x^2}{a^2}-\frac{y^2}{c^2-a^2}=1\]
Det er vanlig å sette c2−a2 = b2, og ligningen for hyperbelen blir da
\[\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\]
I hyperbelens toppunkter er y = 0 og x = ±a. Avstanden mellom de to toppunktene A2 og A1 er altså lik den konstante lengden 2a nevnt ovenfor.
Hyperbelen består av to atskilte grener, og når x blir større, nærmer disse grenene seg to rette linjer gjennom hyperbelens sentrum, asymptotene. Ligningen for asymptotene er
\[y=\pm\frac{b}{a}x\]
Hyperbelen er et kjeglesnitt med eksentrisitet større enn 1. Eksentrisiteten e er lik forholdet mellom brennpunktenes avstand 2c og toppunktenes avstand 2a, det vil si \(e=\frac{c}{a}\). Eksentrisiteten bestemmer vinkelen mellom asymptotene. Hvis vinkelen er 90°, sies hyperbelen å være likesidet.



Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.