grense (matematikk)

Dersom et tall \(a\) ikke er nøyaktig bestemt, men man vet at det ligger mellom to gitte tall, så kalles disse to tall øvre og nedre grense for \(a\).

For eksempel gav Arkimedes de øvre og nedre grenser \(3 \frac17\) og \(3 \frac{10}{71}\)for tallet \(\pi\), som betegner forholdet mellom omkretsen og diameteren til en sirkel, det vil si at vi har at \(3 \frac17 <\pi < \frac{10}{71}\).

Temperaturen \(T\) for vann må ligge mellom 0 °C (ellers blir det til is) og 100 °C (ellers blir det damp), og vi kan kalle disse temperaturene for grenser for mulige vanntemperaturer.

En tallfølge (se følge) \(a_1,a_2,\dots, a_n,\dots\) sies å nærme seg en grense hvis det eksisterer et tall \(a\) slik at \(a_n\) kan komme vilkårlig nær \(a\) når vi kommer tilstrekkelig langt ut i følgen. Mer presist kan vi definere det slik: Til ethvert positivt tall \(\epsilon\), uansett hvor lite, kan vi finne en indeks \(n_0\) som gjør at \(|a_n-a|<\epsilon\) ("vilkårlig nær") for alle \(n>n_0\) ("tilstrekkelig langt ut i følgen"); med andre ord skal differensen \(a_n-a\) i tallverdi bli vilkårlig liten når bare \(n\) gjøres tilstrekkelig stor. Man kaller da \(a\) for tallfølgens grenseverdi og skriver \[a = \lim_{n \to \infty} a_n.\]

Her er lim forkortelse for latin limes, 'grense', og tegnet \(\infty\) betyr uendelig. Selve prosessen å finne grenseverdien kalles en grenseovergang eller en grenseprosess.

Tallfølgen sies å være konvergent hvis det eksisterer en grense, i motsatt fall sies den å være divergent.

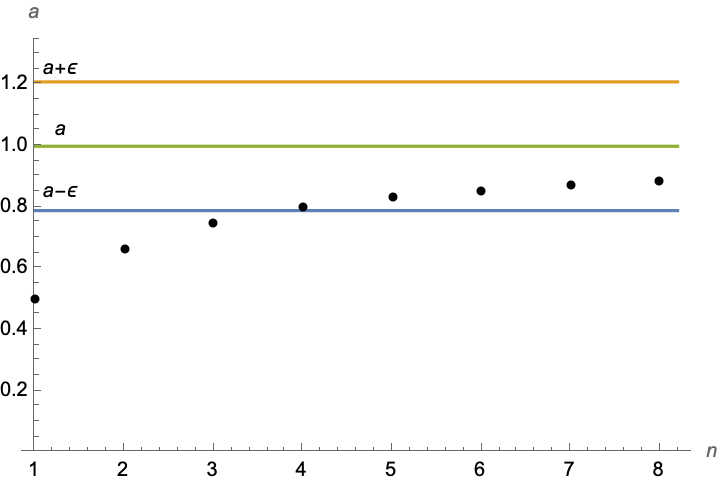
Her er fire eksempler på uendelige tallfølger:

1. Tallfølgen \(1/2,2/3,3/4,\dots, n/(n+1),\dots \) er konvergent med grenseverdien 1. Dette kan vi vise som følger: Vi har at \(|a_n-a|=|n/(n+1)-1|=1/(n+1)\). Om vi har (lite) positivt tall \(\epsilon\), og vi skal ha \(|a_n-a|=1/(n+1)<\epsilon\), må vi ha at \(n>\frac1\epsilon-1\). Det betyr at om vi velger et vilkårlig heltall \(n_0\ge \frac1\epsilon-1\), så har vi for alle \(n>n_0\) at \(|a_n-a|<\epsilon\). Se figur.
2. Tallfølgen \(1,1/2,1/3,1/4,\dots,1/n,\dots\) er konvergent med grenseverdien 0.
3. Tallfølgen \(1,2,3,\dots, n,\dots\) er divergent.
4. Tallfølgen +1, −1, +1, −1, ... er divergent.

Egenskapene ved grenseoverganger studeres i matematiske analyse. Blant de mest alminnelige grenseoverganger kan nevnes summering av uendelige rekker.

En rekke \(a_1+a_2+\cdots+a_n+\cdots\) sies å være konvergent og ha summen \(s\) dersom tallfølgen \(s_1=a_1\), \(s_2=a_1+a_2\), \(s_3=a_1+a_2+a_3\), ... har grenseverdien \(s\). I motsatt fall sies rekken å være divergent.

Vi kan også studere grenseoverganger for funksjoner. En (entydig) funksjon \(f(x)\) sies å ha en grense \(A\) i et punkt \(a\) hvis \[\lim_{n \to \infty} f(a_n) = A\] for enhver tallfølge \(a_1,a_2, \dots\) med grenseverdien \(a\); det vil si når \(x\) nærmer seg \(a\), skal funksjonsverdiene \(f(x)\) nærme seg \(A\). Man skriver da \[\lim_{x \to a} f(x) = A.\]

Alternativt kan vi si at \(\lim_{x \to a} f(x) = A\) dersom det for alle positive tall \(\epsilon\) fins en positiv \(\delta\) (som vil avhenge av \(\epsilon\)) slik at for alle \(x\) med \(|x-a|<\delta\), så vil \(|f(x)-A|<\epsilon\).

En rekke av de viktigste begreper både innen reell og kompleks analyse er definert ved slike grenseprosesser, for eksempel er den deriverte funksjon \(f'(x)\) definert som grenseverdien \[f'(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h}.\]

Grensebegrepet i matematikk har vært vanskelig i mange århundrer, og det var først med Augustin Louis Cauchy og Karl Weierstrass at vi fikk den presise definisjonen av grenser, ofte omtalt som \(\epsilon,\delta\)-argumenter, som vi har brukt her.

• matematiske analyse