Fourierrekker er matematiske rekker der leddene inneholder sinus- og cosinusfunksjoner.
Faktaboks
- Uttale
- furjˈe-
- Etymologi
-
etter Joseph Fourier
- Også kjent som
- trigonometriske rekker, Fourier-rekker
En fourierrekke kan skrives på formen \[\frac12 A_0+A_1\cos x+A_2 \cos 2x+\cdots +B_1\sin x+B_2 \sin 2x+\cdots,\] eller med summetegn \[\frac12 A_0+\sum_{n=1}^\infty\big(A_n\cos (nx)+B_n\sin (nx) \big).\] Navnet skyldes at Joseph Fourier brukte rekkene som grunnlag for beregninger av varmeledning.
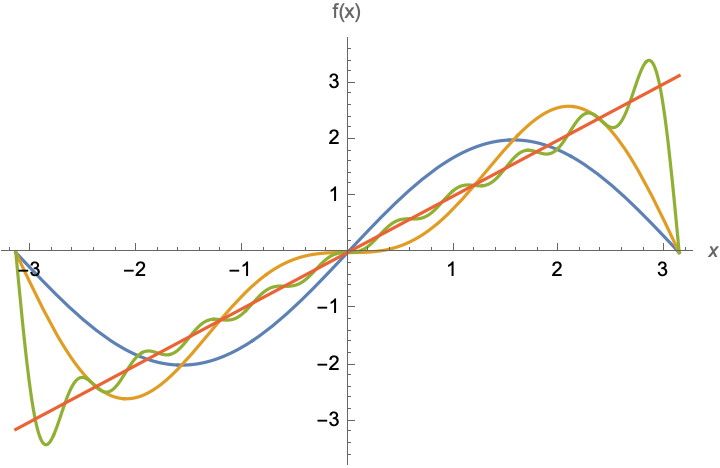
Ta funksjonen \(f(x)=x\) for \(x\in(-\pi,\pi)\) som eksempel. Figuren viser fourierrekken for ett, to og ti ledd. (I summen ovenfor erstatter vi "\(\infty\)" med henholdsvis 1, 2, og 10.) Vi ser at jo flere ledd vi tar med, jo nærmere kommer vi funksjonen. Men vi ser også oscillasjoner som er typiske for fourierrekker.




Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.