Det gylne snitt er en måte å dele et linjestykke på slik at de to delene står i et bestemt forhold til hverandre og til helheten.
Det gylne snitt har blitt brukt som grunnlag for komposisjon av bilder og arkitektur siden antikken, og har blitt oppfattet som en vakker og harmonisk måte å dele opp en bildeflate på.
Det gylne snitt er en oppdeling av et linjestykke i to deler slik at forholdet mellom hele linjestykket og den største delen er det samme som forholdet mellom den største delen og den minste.
Med symboler kan dette skrives slik: Dersom linjestykket har lengde a og den største delen har lengde x, får man ligningen
\(a : x = x : (a-x) \)
Dette gir
\(a=x\cdot\frac{1+\sqrt{5}}{2}\)
Det gylne snitt symboliseres ofte med den greske bokstaven φ (phi) og er et irrasjonalt tall med verdi
\(\varphi = {1 + \sqrt{5} \over 2}\approx\ 1,618034\)
Uttrykket gir en enkel konstruksjon av x ved hjelp av en rettvinklet trekant der katetene har lengde a og \(\frac{a}{2}\); se figuren.
Forholdstallet \(\varphi=\frac{1}{2}\left(1+\sqrt{5}\right)\) har flere interessante egenskaper. Det har kjedebrøksutviklingen \[\varphi=1+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{1+\dots}}}=1,618034\dots\] (se kjedebrøk) med de beste tilnærmelsesbrøkene
\(1, \frac{2}{1}, \frac{3}{2}, \frac{5}{3}, \frac{8}{5}, \dots\)
Tallene 1, 1, 2, 3, 5, 8, ... som forekommer her, er fibonaccitallene, der hvert tall er summen av de to foregående (se Leonardo Fibonacci).
Både selve forholdstallet \(\varphi\) i det gylne snitt og tilnærmelsesbrøkene forekommer på forskjellig måte i naturen, for eksempel ved bladstillingen på planter eller som forholdstall ved spiralene på sneglehus og så videre.
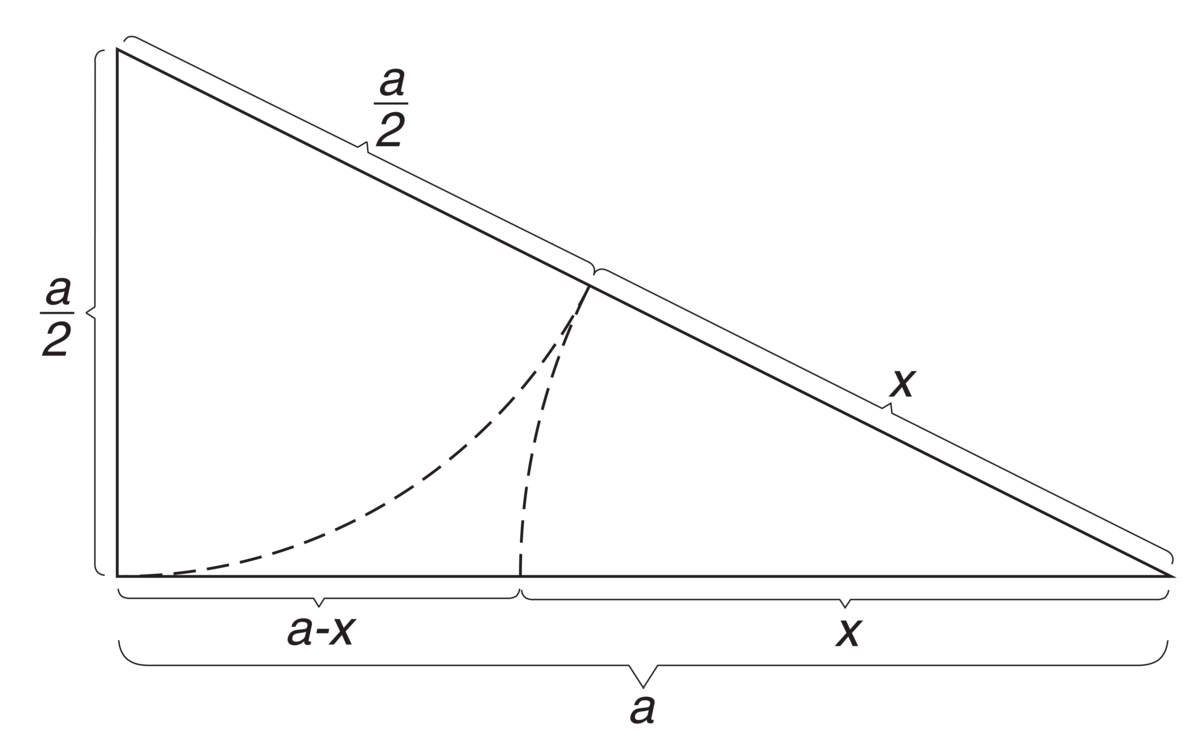
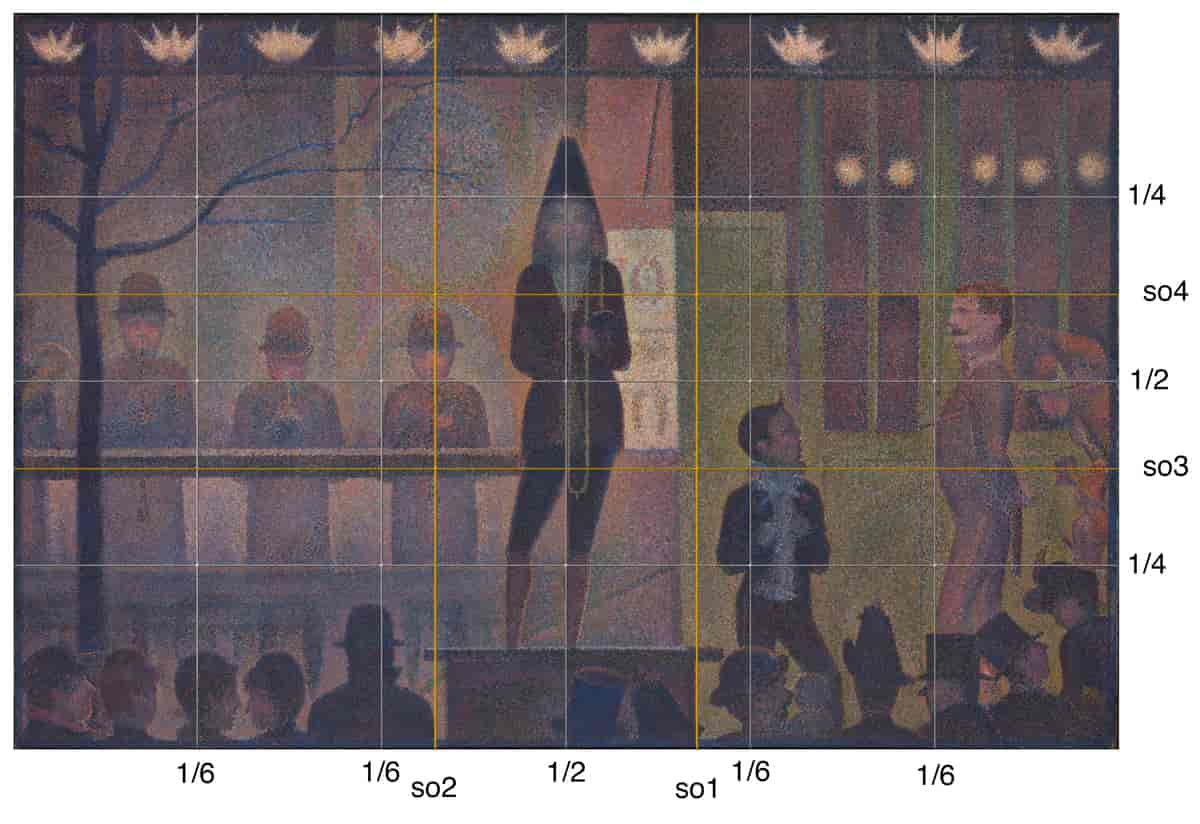
Det gylne snitt var tidlig kjent og ansett for å ha særlig betydning i den klassiske greske matematikken. Det finnes blant annet forskjellige mer eller mindre vel underbygde teorier for betydningen det gylne snitt skal ha for estetiske og kunstneriske oppgaver.
Det gylne snitt forekommer ofte i kunst og arkitektur. Fronten på Parthenon-tempelet på Akropolis kan innskrives i et gyllent rektangel (det ødelagte taket er tegnet inn på bildet med svart), og forholdet går igjen i en lang rekke detaljer i utformingen av tempelet, søylene og dekorasjonene.
Det gylne snitt har vært brukt i komposisjon siden antikken, i renessansen og senere. Slike proporsjoner mente man hadde en balanse som på en naturlig måte tiltaler menneskets øye og sinn. Spesielt ble det gylne snitt rettferdiggjort av naturen selv, fordi proporsjonene kan iakttas hos planter og dyr.
Prinsippet går i hovedtrekk ut på at hvis man deler et billedutsnitt i ni like store deler ved å dele det i tre både horisontalt og vertikalt, er de gylne snittene de fire krysningspunktene for delingslinjene. Motivet bør plasseres i et av disse.
Det gylne snitt ble også mye brukt i arkitekturen, og i geometriske systemer kan man lage arkitektoniske systemer oppbygd etter visse prinsipper fra det gylne snitt og lignende konstruksjoner.
I Norge ble diskusjonen av slike geometriske systemer aktuell gjennom Fredrik Macody Lunds bok Ad quadratum (1919), hvor han søkte å bevise at Nidarosdomen i hovedtrekk er bygd etter et slikt system.
Kommentarer (4)
skrev Lars Nygaard
svarte Gunn Hild Lem
skrev Magnus Skrunes
I beskrivelsen av matematiske egenskaper har man oppgitt φ galt. Det skal være pluss i parentesen, noe som også gjør at den oppgitte kjedebrøken må endres slik at et ettall kommer først pluss den oppgitte kjedebrøk.
svarte Jon Eivind Vatne
Hei
Jeg er enig i det du skriver, og har oppdatert artikkelen. Merk at den opprinnelige formuleringen var korrekt for inversen av det gyldne snitt, som også er lik det gyldne snitt minus en.
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.