derivere

Om \(y=f(x)\) betegner posisjonen til bil på en vei ved tiden \(x\), vil den deriverte av \(y'=f'(x)\) betegne hastigheten til bilen ved tid \(x\). Den andrederiverte \(y''=f''(x)\) vil betegne akselerasjonen.

Dette kan forstås på følgende måte: Anta at bilens posisjon blir målt ved tiden \(x_1\) og litt senere ved tiden \(x_2\). Vi finner posisjonene \(f(x_1)\) og \(f(x_2)\) på disse tidspunktene. Avstanden bilen har beveget seg, er \(f(x_2)-f(x_1)\) i løpet av tiden \(x_2-x_1\). Da blir den gjennomsnittlige hastigheten \((f(x_2)-f(x_1))/(x_2-x_1)\). Om vi reduserer tidsintervallet, vil vi få en mer presis angivelse av hastigheten i øyeblikket. I grensen får vi den momentane hastigheten som vi leser av på speedometeret, og som altså er den deriverte av funksjonen som angir posisjonen som funksjon av tiden, dvs at hastigheten til bilen ved tid \(x\) er \(f'(x)\).

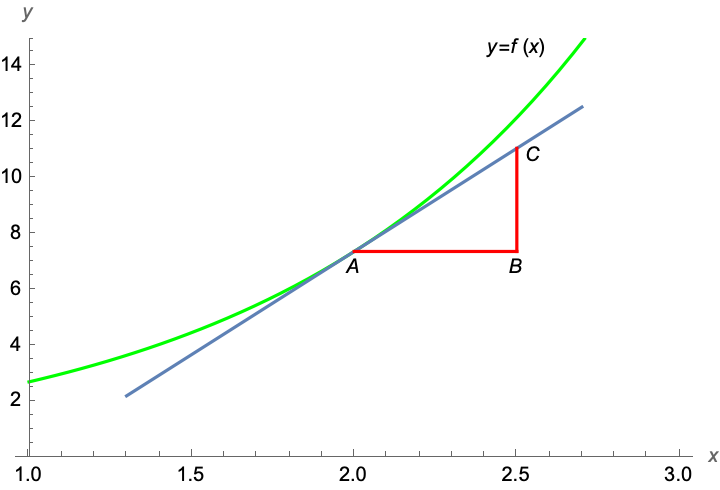
Den deriverte av en funksjon har også en grafisk tolkning. Hvis man tegner grafen til en funksjon, viser den deriverte hvor bratt denne grafen er. Den deriverte til funksjonen i ett bestemt punkt er lik stigningstallet til tangenten til grafen til funksjonen i dette punktet.

Matematisk uttrykkes dette som at vi studerer grensen for \((f(x_2)-f(x_1))/(x_2-x_1)\) når \(x_2-x_1\) går mot null. Dette skrives som \[y'=f'(x_1)=\lim_{x_2\to x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1}.\] Grensen kalles for den deriverte til \(y\) i punktet \(x_1\).

Mer generelt er en funksjon \(y=f(x): {\mathbb R}\to {\mathbb R}\) deriverbar i \(x\) hvis grenseverdien \[\lim_{h\to 0}\frac{1}{h}(f(x+h)-f(x))\] eksisterer. Denne grensen kalles den deriverte av \(y\) i \(x\). Dette skrives \[y'=f'(x)=\lim_{h\to 0}\frac{1}{h}(f(x+h)-f(x)).\]

Den matematiske analysen (kalkulus) ble utviklet av Isaac Newton og Gottfried Wilhelm Leibniz på midten av 1700-tallet. Her spiller den deriverte en helt sentral rolle.

• differensialregning
• funksjon