fouriertransformen

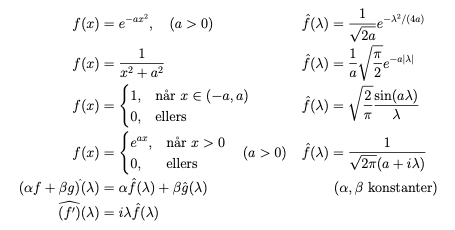
Fouriertransformasjonen \(\hat{\, f}\) av en funksjon \(f\) med definisjonsmengde de reelle tallene og billedmengde de komplekse tallene, er definert ved \[\hat{\,f}(\lambda)=\frac1{\sqrt{2\pi}}\int_{-\infty}^\infty f(x)e^{-ix\lambda}\, dx\] Her er e Eulers konstant og i den imaginære enhet.

Det er tre naturlige funksjonsrom der fouriertransformasjonen er veldefinert, nemlig

1. rommet \(L^1\) av de integrerbare funksjoner (der absoluttverdien av funksjonen har et endelig integral over de reelle tallene)
2. rommet \(L^2\) av de kvadratisk integrerbare funksjoner (der absoluttverdien kvadrert av funksjonen har et endelig integral over de reelle tallene)
3. Schwartz-rommet \(\mathcal S\) av de funksjonene som sammen med alle sine deriverte avtar raskere mot uendelig enn den inverse til et vilkårlig polynom

Man kan også definere fouriertransformen for funksjoner av flere variable og for periodiske funksjoner.

Dersom man kjenner den fouriertransformerte \(\hat{\,f}\) til en funksjon \(f\), kan man finne igjen funksjonen ved hjelp av den inverse fouriertransformasjonen\[f(x)=\frac1{\sqrt{2\pi}}\int_{-\infty}^\infty\hat{\,f}(\lambda) e^{ix\lambda}\, d\lambda.\]

Noen eksempler er gitt i tabellen ved siden av. Det er bare én funksjon, nemlig \(f(x)=e^{-x^2/2}\), som er lik sin fouriertransformerte, dvs \(f=\hat{\,f}\), i tillegg til den trivielle funksjonen \(f(x)=0\).

Fouriertransformasjonen har en rekke nyttige egenskaper, for eksempel at funksjonen og dens fouriertransformerte har samme norm i \(L ^2\). En veldig nyttig egenskap ved fouriertransformen er formelen for den fouriertransformerte av den deriverte av en funksjon, se tabellen.

Av stor viktighet i kvantemekanikken er Heisenbergs usikkerhetsrelasjon, som er identisk med ulikheten\[\Big(\int_{-\infty}^\infty x^2 |f(x)|^2 \, dx\Big) \Big(\int_{-\infty}^\infty \lambda^2 |\hat{\,f}(\lambda)|^2 \, d\lambda\Big)\ge \frac14 \Big(\int_{-\infty}^\infty |f(x)|^2 \, dx\Big)^2\]

Innen digitalteknikk har også fouriertransformasjonen viktige anvendelser, se for eksempel FFT (Fast Fourier Transform).

• fourieranalyse
• FFT
• matematisk analyse