Akhillevs og skilpadden – Store norske leksikon

Akhillevs og skilpadden er et av Zenon fra Eleas' argumenter mot at bevegelse er mulig. Zenons argument kan gjengis som følger:

Faktaboks

Uttale: akhˈillevs og skilpadden
Også kjent som: akhillevsargumentet

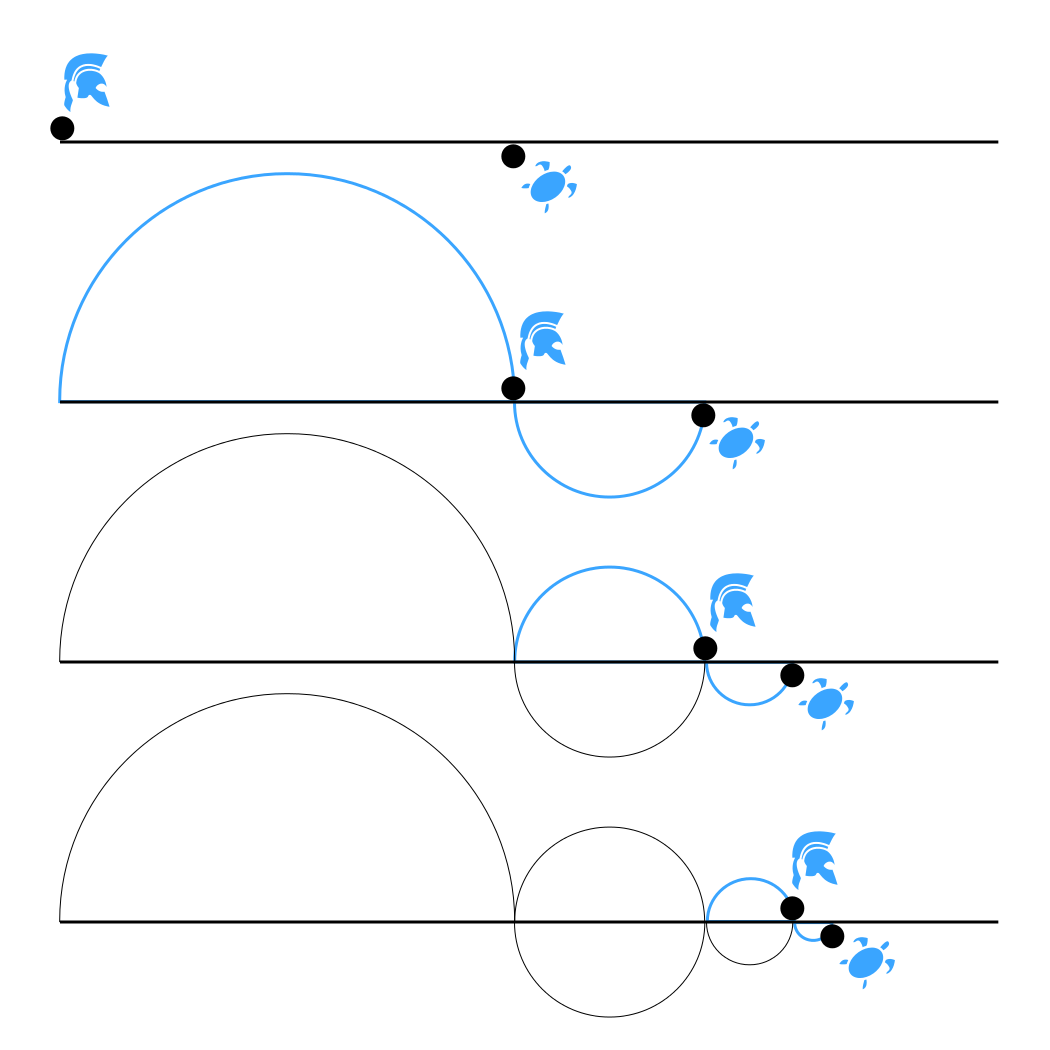
«Hvis bevegelse er mulig, kan selv ikke Akhillevs, den hurtigste løper i Hellas, nå igjen en skilpadde som starter før ham. Akhillevs starter fra punkt p₁ når skilpadden er kommet til punkt p₂, men uansett hvor kort tid Akhillevs bruker på å nå p₂, er skilpadden på den tiden kommet et lite stykke lenger, til p₃, og så videre. Avstanden mellom dem går mot null, men blir aldri null. Denne sistnevnte konklusjonen er imidlertid absurd. Siden denne konklusjonen er en konsekvens av antagelsen av at bevegelse er mulig, er derfor denne antagelse selv absurd».

Zenon mener med dette å ha bevist at bevegelse er umulig. Dette kalles akhillevsargumentet eller på latin: argumentum Achilleum.

Les mer i Store norske leksikon

Kommentarer (2)

3. mars 2009 skrev Harry Johansen

Det kunne nok vært ført et bedre argument for at antagelsen er absurd enn det som gjøres her. Om artikkelforfatteren hadde fylgt med i fysikktimene og lært formelen for hastighet, som er v(hastighet)= s(strekning)/t(tid)ville han sett at hans logiske argumentasjon for antagelsens absurditet er en smule mangelfull. For ikke å si en meget mangelfull all den tid den bare ser på to forhold ved bevegelse. Men sånn kan det gå.Harry

1. desember 2010 svarte Thomas Østerhaug

Jeg kan ikke se at artikkelforfatteren noe sted argumenterer for at antagelsen er absurd. Det er en gjengivelse av Zenons argument, og Zenon hadde neppe fysikktimer å følge med i.

Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.

Du må være logget inn for å kommentere.

Fagansvarlig for Antikkens filosofi

Hallvard Fossheim

Professor, Universitetet i Bergen