komplekse tall

Et komplekst tall defineres som et element på formen a + ib, hvor a og b er reelle tall. Man kaller a realdelen og b imaginærdelen av det komplekse tallet a + ib. Dersom a = 0, sies tallet å være rent imaginært eller bare et imaginært tall. Dersom b = 0, er tallet et reelt tall.

Tallet a – ib kalles den komplekskonjugerte til a + ib.

For regning med komplekse tall gjelder følgende regler:

\((a_1 + ib_1) \pm (a_2 + ib_2) = (a_1 \pm a_2) + i(b_1 \pm b_2)\)

\((a_1 + ib_1)(a_2 + ib_2) = (a_1a_2 – b_1b_2) + i(b_1a_2 + b_2a_1)\)

\(\frac{a_1 + ib_1}{a_2 + ib_2} = \frac{\left(a_1 a_2 + b_1 b_2\right) + i\left(a_2 b_1 – a_1 b_2\right)}{a_2^2 + b_2^2}\)

Ifølge disse regnereglene danner de komplekse tallene en kropp. Enhver ligning av formen \(a_0x^n + a_1x^{n-1} + \dots + a_n = 0\), hvor \(a_0, a_1, \dots, a_n\) er komplekse tall, har løsninger innenfor mengden av de komplekse tall.

De reelle tallene avbildes ofte som punkter på en linje, den reelle tallinjen. Komplekse tall kan avbildes geometrisk ved hjelp av det komplekse tallplanet (også kalt det gaussiske tallplan, etter Carl Friedrich Gauss). Dette er et rettvinklet koordinatsystem hvor den horisontale aksen (abscissen) er den reelle tallinjen, med enhet lik 1, og den vertikale aksen er den imaginære aksen, med enhet lik i. Da kan det komplekse tallet a + ib markeres i planet som et punkt med koordinatene (a, b).

Man kan også bruke polarkoordinater. Da oppfattes det komplekse tallet som en vektor av lengde r med begynnelsespunkt i origo og endepunkt i (a, b). Størrelsen kalles absoluttverdien, modulen eller tallverdien til a + ib, og man skriver \(r = |a + ib| =\sqrt{a^2 + b^2}\).

Vinkelen φ (den greske bokstaven fi) som vektoren danner med den reelle aksen, kalles amplituden eller argumentet til det komplekse tallet. Den er bestemt ved \(\tan{\phi}=\frac{b}{a}\).

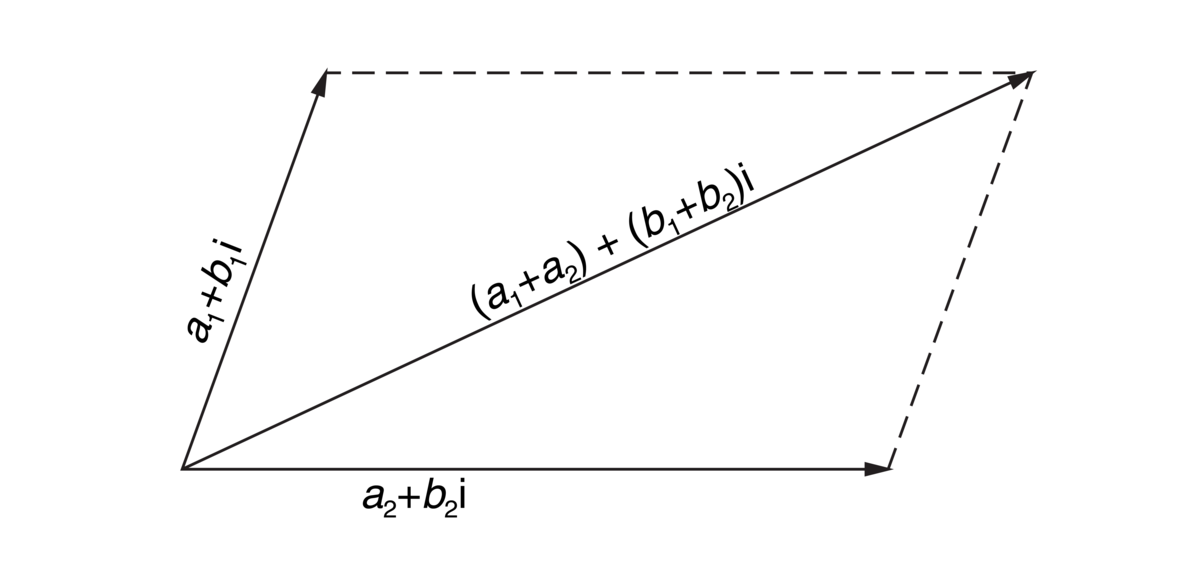
Summen av to komplekse tall kan fremstilles geometrisk ved vektoraddisjon (geometrisk addisjon). Det vil si at summen blir representert ved diagonalen i det parallellogrammet som blir dannet av de to aktuelle vektorene.

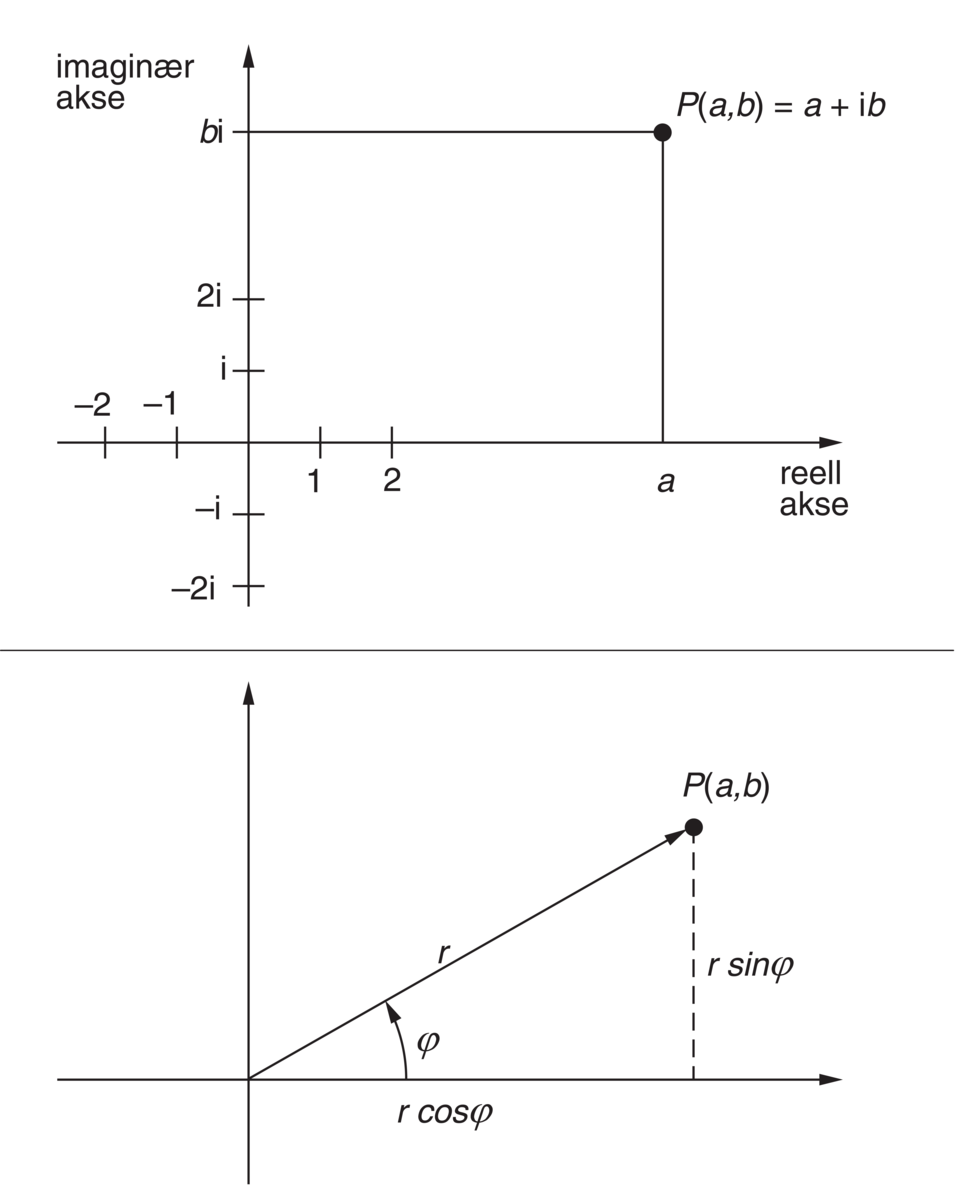
Ved hjelp av absoluttverdien av disse størrelsene kan komplekse tall skrives på trigonometrisk form:

\[a + ib = r (\cos \phi + i \sin \phi)\]

Dersom man multipliserer de to komplekse tallene \(a + ib = r(\cos \phi + i \sin \phi)\) og \(a_1 + ib_1 = r_1(\cos \phi_1 + i \sin \phi_1)\) på trigonometrisk form, finner man følgende formel:

\[(a + ib)(a_1 + ib_1) = rr_1[\cos (\phi + \phi_1) + i \sin (\phi + \phi_1)]\]

For flere like faktorer kommer man frem til de Moivres formel:

\[(\cos \phi + i \sin \phi)^n = \cos n\phi + i \sin n\phi\]

Den eksponentielle formen for komplekse tall ble innført av Leonhard Euler, og uttrykkes i identiteten \(a + ib = r(\cos \phi + i \sin \phi) = r \cdot e^{i\phi}\), der e er grunntallet i det naturlige logaritmesystemet.

Et komplekst tall a + ib sies å være helt hvis a og b er heltall. For hele komplekse tall kan man utvikle en tallteori som nøye svarer til den vanlige teori for hele tall. Ethvert helt komplekst tall kan skrives entydig som et produkt av primfaktorer. Tallteorien for komplekse tall ble utviklet av Carl Friedrich Gauss.

De hyperkomplekse tallene er tallsystemer som man kan betrakte som generalisering av komplekse tall.

Komplekse tall forekommer først i den italienske matematikeren og legen Girolama Cardanos Ars Magna (1545), men Cardano forstod ikke begrepet fullt ut. René Descartes benyttet uttrykket imaginære røtter. Til dels bruker man ennå betegnelsen imaginære tall i samme betydning som komplekse tall. Symbolet for komplekse tall ble fastsatt av Leonhard Euler.

Den geometriske fremstillingen av komplekse tall ble først innført av den dansk-norske landmåleren Caspar Wessel i avhandlingen «Om directionens analytiske betegnelse», fremlagt for Det Danske Videnskabernes Selskab i 1797, trykt 1799. Wessels arbeid ble ikke videre lagt merke til, og noen år senere ble samme metode benyttet av Jean Robert Agand og Carl Friedrich Gauss.

De komplekse tallene danner grunnlaget for kompleks analyse (funksjonsteori), som blant annet handler om differensialregning og integralregning for funksjoner av en eller flere komplekse variabler.

• reelle tall
• matematisk analyse